题目内容

18．经过点C（2，-3），且与两点M（1，2）和N（-1，-5）距离相等的直线方程是7x-2y-20=0或3x+4y+6=0．

分析 分类讨论：当要求的直线与MN平行时，当要求的直线经过线段MN的中点P$（0，-\frac{3}{2}）$时，即可得出．

解答 解：①当要求的直线与MN平行时，kMN=$\frac{-5-2}{-1-1}$=$\frac{7}{2}$，可得直线方程为：y+3=$\frac{7}{2}$（x-2），化为：7x-2y-20=0．
②当要求的直线经过线段MN的中点P$（0，-\frac{3}{2}）$时，kPC=$\frac{-3-（-\frac{3}{2}）}{2-0}$=-$\frac{3}{4}$，可得直线方程为：y+3=-$\frac{3}{4}$（x-2），化为：3x+4y+6=0．
故答案为：7x-2y-20=0或3x+4y+6=0．

点评 本题考查了相互平行的直线斜率之间的关系、中点坐标公式、直线方程，考查了分类讨论方法、推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
8．已知各项均为正数的数列{an}满足：an+1=$\frac{\sqrt{{a}_{n}}}{2}$+$\frac{1}{2}$（n∈N+）．
（1）若（a1-1）（a2-2）＜0，求a1的范围；
（2）设max{a，b}表示a、b两数中较大的数．试证明：对任意的n∈N+，都有an≤max{1，a1}．
9．已知各项为正的等比数列{an}的前n项和为Sn，S4=30，过点P（n，log2an）和Q（n+2，log2an+1）（n∈N*）的直线的斜率为1，设bn=$\frac{lo{g}_{2}{a}_{n+1}}{lo{{g}_{2}}^{2}{a}_{n+2}•lo{{g}_{2}}^{2}{a}_{n}}$，则数列{bn}的前n项和Tn=$\frac{1}{8}$（$\frac{1}{lo{{g}_{2}}^{2}\frac{6}{17}}$+$\frac{1}{lo{{g}_{2}}^{2}\frac{24}{17}}$-$\frac{1}{lo{{g}_{2}}^{2}（\frac{6}{17}•{4}^{n}）}$-$\frac{1}{lo{{g}_{2}}^{2}（\frac{6}{17}•{4}^{n+1}）}$）．
6．已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2+2x，则当x＜0时，f（x）=-x2+2x．
13．$\frac{2co{s}^{2}α-1}{2tan（\frac{π}{4}-α）si{n}^{2}（\frac{π}{4}+α）}$=（　　）
A．1B．2C．3D．4
3．已知集合A={x|y=lg$\frac{1+x}{1-x}$}，集合B={x|a＜x＜a+1}，若B⊆A，求实数a的取值范围．
10．已知三棱柱ABC-A1B1C1的底面是锐角三角形，则存在过点A的平面（　　）
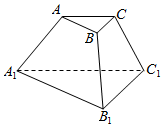
A．与直线BC和直线A1B1都平行B．与直线BC和直线A1B1都垂直
C．与直线BC平行且直线A1B1垂直D．与直线BC和直线A1B1所成角相等
7．已知函数f（x）=4cosxsin（x+$\frac{π}{6}$）-1．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）在钝角△ABC，内角A，B，C的对边分别为a，b，c，且f（B）=1，若b=$\sqrt{13}$，c=4，求a的值．
8．已知点A（4，0），抛物线C：x2=12y的焦点为F，射线FA与抛物线和它的准线分别相交于点M和N，则|FM|：|MN|等于（　　）
A．2：3B．3：4C．3：5D．4：5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网