Question

复数z=（3+i）m-（2+i）n（m、n∈R）对应的点在第四象限内，则

m

n

的取值范围是

2

3

＜

m

n

＜1

．

Answer 1

分析：化简复数的为a+bi的形式，利用对应点所在象限，得到可行域，然后求出

m

n

的取值范围．

解答：解：复数z=（3+i）m-（2+i）n=（3m-2n）+（m-n）i，（m、n∈R）对应的点在第四象限内，
即

3m-2n＞0 m-n＜0

，画出约束条件的可行域，如图，

m

n

相当于直线的斜率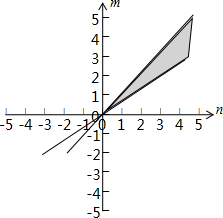，所以

2

3

＜

m

n

＜1．
故答案为：

2

3

＜

m

n

＜1．

点评：本题以复数为载体考查线性规划知识，基本知识的应用．