题目内容

9．实系数方程x2+ax+2b=0的两根为x1，x2，且0≤x1≤1≤x2≤2，则a2-2a+b2-4b+5的最小值是（　　）
A．8B．9C．$\frac{36}{5}$D．6

分析 由题意可推出a，b 满足的条件，画出约束条件的可行域，结合a2-2a+b2-4b+5=（a-1）2+（b-2）2 的几何意义，求出即可

解答 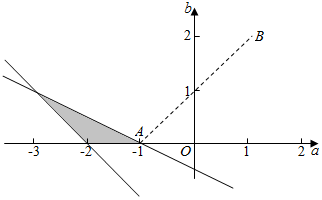解：实系数方程x2+ax+2b=0的两根为x1，x2，且0≤x1≤1≤x2≤2，
∴$\left\{\begin{array}{l}{1+a+2b≤0}\\{2b≥0}\\{4+2a+2b≥0}\end{array}\right.$，
∵a2-2a+b2-4b+5=（a-1）2+（b-2）2，
∴其几何意义是，约束条件内的点与B（1，2）连线的距离，画出可行域如图，点A（-1，0）为最优解，
∴当a=-1，b=0时，有最小值，即为4+4=8，
故选：A．

点评 本题主要考查一元二次方程根的分布与系数的关系，体现了转化、数形结合的数学思想．还考查线性规划的应用，考查计算能力．注意正确做出约束条件的可行域，是解题的关键．

练习册系列答案
相关题目
19．已知函数f（x）是定义在R上的奇函数，且对任意0＜x1＜x2时，都有（x1-x2）[f（x1）-f（x2）]＞0，若关于x的不等式f（x2-2mx+m+1）+f（x2-1）＜0的解集中恰好有两个整数，则实数m的取值范围是$（1-\sqrt{10}，1-\sqrt{2}）∪$$（1+\sqrt{2}，1+\sqrt{10}）$．
20．已知椭圆有如下性质：F是椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点，直线l：x=$\frac{{a}^{2}}{c}$为C的右准线，点P是椭圆上的任意一点，设d表示P到l的距离，那么可得$\frac{|PF|}{d}$=t（t为定值）．类比椭圆的上述性质，双曲线$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{3}$=1上一点P到右焦点F与右准线的距离d之比为（　　）
A．$\frac{1}{2}$B．$\sqrt{2}$C．2D．$\frac{\sqrt{7}}{2}$
17．光线沿着直线y=-3x+b射到直线x+y=0上，经反射后沿着直线y=ax+2射出，则有（　　）
A．a=$\frac{1}{3}$，b=6B．a=-$\frac{1}{3}$，b=-6C．a=3，b=-$\frac{1}{6}$D．a=-3，b=$\frac{1}{6}$
4．锐角三角形ABC中，角A，B，C所对的边分别为a，b，c，且c-a（cosB+$\frac{\sqrt{3}}{3}$sinB）=0．
（1）求角A的大小；
（2）若a=$\sqrt{3}$，求△ABC周长的取值范围．
14．满足z2=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i的复数z=$\frac{\sqrt{3}}{2}+\frac{1}{2}i$或-$\frac{\sqrt{3}}{2}-\frac{1}{2}i$．
1．若${C}_{n}^{0}$+$\frac{1}{2}$${C}_{n}^{1}$+$\frac{1}{3}$${C}_{n}^{2}$+…+$\frac{1}{n+1}$${C}_{n}^{n}$=$\frac{31}{n+1}$，求（1-2x）2n的展开式中系数最大的项．
18．已知等差数列{an}的前n项和为Sn，且$\frac{{S}_{25}}{{a}_{23}}$=5，$\frac{{S}_{45}}{{a}_{33}}=25$，则$\frac{{S}_{65}}{{a}_{43}}$等于（　　）
A．125B．85C．45D．35
16．设a=0.5${\;}^{\frac{1}{2}}$，b=0.8${\;}^{\frac{1}{2}}$，c=log20.5，则a、b、c的大小关系是（　　）
A．c＜b＜aB．c＜a＜bC．a＜b＜cD．b＜a＜c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网