题目内容
已知动点P到点A(-2,0)与点B(2,0)的斜率之积为-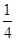 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.
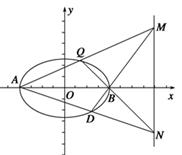
(1)求曲线C的方程;
(2)若点Q为曲线C上的一点,直线AQ,BQ与直线x=4分别交于M,N两点,直线BM与椭圆的交点为D.求证,A,D,N三点共线.
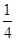 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)若点Q为曲线C上的一点,直线AQ,BQ与直线x=4分别交于M,N两点,直线BM与椭圆的交点为D.求证,A,D,N三点共线.
(1)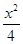 +y2=1(x≠±2).(2)见解析
+y2=1(x≠±2).(2)见解析
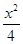 +y2=1(x≠±2).(2)见解析
+y2=1(x≠±2).(2)见解析(1)解 设P点坐标(x,y),则kAP=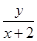 (x≠-2),kBP=
(x≠-2),kBP=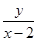 (x≠2),由已知
(x≠2),由已知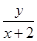 ·
·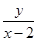 =-
=-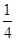 ,化简,得
,化简,得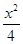 +y2=1,所求曲线C的方程为
+y2=1,所求曲线C的方程为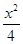 +y2=1(x≠±2).
+y2=1(x≠±2).
(2)证明 由已知直线AQ的斜率存在,且不等于0,设方程为y=k(x+2),
由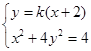 消去y,得(1+4k2)x2+16k2x+16k2-4=0,①
消去y,得(1+4k2)x2+16k2x+16k2-4=0,①
因为-2,xQ是方程①的两个根,所以-2xQ=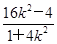 ,得xQ=
,得xQ=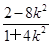 ,又yQ=k(xQ+2)=k
,又yQ=k(xQ+2)=k =
=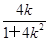 ,所以Q
,所以Q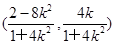 .
.
当x=4,得yM=6k,即M(4,6k).
又直线BQ的斜率为-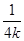 ,方程为y=-
,方程为y=-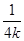 (x-2),当x=4时,得yN=-
(x-2),当x=4时,得yN=-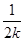 ,即N
,即N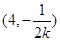 .直线BM的斜率为3k,方程为y=3k(x-2).
.直线BM的斜率为3k,方程为y=3k(x-2).
由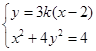 消去y得:
消去y得:
(1+36k2)x2-144k2x+144k2-4=0,②
因为2,xD是方程②的两个根,
所以2·xD=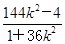 ,
,
得xD=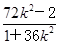 ,又yD=3k(xD-2)=-
,又yD=3k(xD-2)=-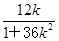 ,
,
即D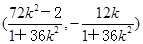 ,
,
由上述计算:A(-2,0),
D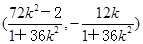 ,N
,N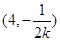 .
.
因为kAD=-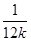 ,kAN=-
,kAN=-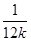 ,所以kAD=kAN.
,所以kAD=kAN.
所以A,D,N三点共线.
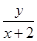 (x≠-2),kBP=
(x≠-2),kBP=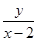 (x≠2),由已知
(x≠2),由已知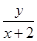 ·
·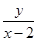 =-
=-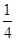 ,化简,得
,化简,得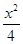 +y2=1,所求曲线C的方程为
+y2=1,所求曲线C的方程为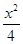 +y2=1(x≠±2).
+y2=1(x≠±2).(2)证明 由已知直线AQ的斜率存在,且不等于0,设方程为y=k(x+2),
由
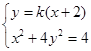 消去y,得(1+4k2)x2+16k2x+16k2-4=0,①
消去y,得(1+4k2)x2+16k2x+16k2-4=0,①因为-2,xQ是方程①的两个根,所以-2xQ=
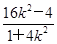 ,得xQ=
,得xQ=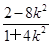 ,又yQ=k(xQ+2)=k
,又yQ=k(xQ+2)=k =
=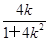 ,所以Q
,所以Q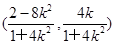 .
.当x=4,得yM=6k,即M(4,6k).
又直线BQ的斜率为-
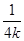 ,方程为y=-
,方程为y=-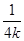 (x-2),当x=4时,得yN=-
(x-2),当x=4时,得yN=-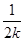 ,即N
,即N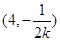 .直线BM的斜率为3k,方程为y=3k(x-2).
.直线BM的斜率为3k,方程为y=3k(x-2).由
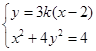 消去y得:
消去y得:(1+36k2)x2-144k2x+144k2-4=0,②
因为2,xD是方程②的两个根,
所以2·xD=
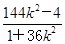 ,
,得xD=
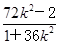 ,又yD=3k(xD-2)=-
,又yD=3k(xD-2)=-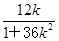 ,
,即D
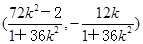 ,
,由上述计算:A(-2,0),
D
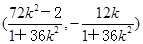 ,N
,N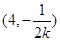 .
.因为kAD=-
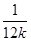 ,kAN=-
,kAN=-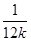 ,所以kAD=kAN.
,所以kAD=kAN.所以A,D,N三点共线.

练习册系列答案
相关题目
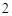 的椭圆
的椭圆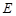 的两个顶点分别为
的两个顶点分别为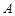 和
和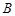 ,且
,且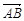 与n
与n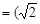 ,
,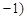 共线.
共线.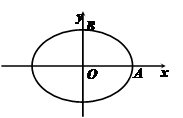
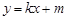 与椭圆
与椭圆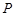 和
和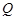 ,且原点
,且原点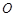 总在以
总在以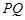 为直径的圆的内部,求实数
为直径的圆的内部,求实数 的取值范围.
的取值范围.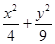 =1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且
=1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且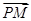 =2
=2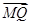 ,点M的轨迹为C.
,点M的轨迹为C.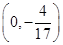 且平行于x轴的直线上一动点,且满足
且平行于x轴的直线上一动点,且满足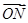 =
=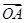 +
+ (O为原点),且四边形OANB为矩形,求直线l的方程.
(O为原点),且四边形OANB为矩形,求直线l的方程. 过椭圆
过椭圆 的左焦点
的左焦点 和一个顶点
和一个顶点 ,则椭圆的方程为 .
,则椭圆的方程为 . 是椭圆
是椭圆 上的一动点,
上的一动点, 为椭圆的两个焦点,
为椭圆的两个焦点, 是坐标原点,若
是坐标原点,若 是
是 的角平分线上的一点,且
的角平分线上的一点,且 ,则
,则 的取值范围为( )
的取值范围为( )



 :
: (a>b>0)的离心率为
(a>b>0)的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 (k>0)的直线于
(k>0)的直线于 、
、 两点,若
两点,若 ,则
,则

 是椭圆上的一点,
是椭圆上的一点,  是焦点, 且, 则△
是焦点, 且, 则△ 的面积是
的面积是



 上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα=
上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα= ,sin(α+β)=
,sin(α+β)= ,则此椭圆的离心率为 .
,则此椭圆的离心率为 .