题目内容
【题目】设{an}是各项都为整数的等差数列,其前n项和为![]() ,
,![]() 是等比数列,且
是等比数列,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设cn=log2b1+log2b2+log2b3+…+log2bn, ![]() .
.
(i)求Tn;
(ii)求证: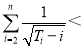 2.
2.
【答案】(1)![]() ,
,![]() ,
,![]() (2)(i)n3(ii)证明见解析;
(2)(i)n3(ii)证明见解析;
【解析】
(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,运用等差数列和等比数列的通项公式,解方程可得公差和公比,即可得到所求通项公式;
(2)(i)运用对数的运算性质和等差数列的求和公式可得![]() ,a
,a![]() n2﹣n﹣1+2i,再由数列的分组求和,结合等差数列的求和公式,计算可得所求和;
n2﹣n﹣1+2i,再由数列的分组求和,结合等差数列的求和公式,计算可得所求和;
(ii)推得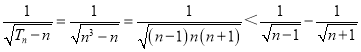 ,再由数列的裂项相消求和,结合不等式的性质,即可得证.
,再由数列的裂项相消求和,结合不等式的性质,即可得证.
解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,由![]() ,
,![]() ,
,![]() ,可得
,可得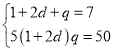 ,
,
解得d=2,q=2或d![]() ,q=5,
,q=5,
由于{an}是各项都为整数的等差数列,所以d=2,q=2,
从而![]() ,
,![]() ,
,![]() ;
;
(2)(i)∵log2bn=log22n﹣1=n﹣1,
∴cn=0+1+2+…+(n﹣1)![]() n(n﹣1),
n(n﹣1),
∴a![]() 2(
2(![]() i)﹣1=n2﹣n﹣1+2i,
i)﹣1=n2﹣n﹣1+2i,
∴Tn=(n2﹣n﹣1+2)+(n2﹣n﹣1+4)+…+(n2﹣n﹣1+2n)
=n(n2﹣n﹣1)+(2+4+…+2n)=n(n2﹣n﹣1)+n(n+1)=n3;
(ii)证明: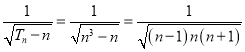
![]()
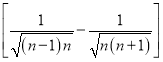
![]()
![]() ,
,
而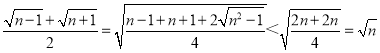 ,
,
∴![]() ,
,
∴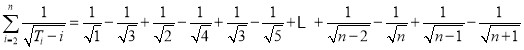
=1![]() ,
,
由于![]() 0,
0,
可得1![]() 2.
2.
则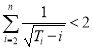 .
.

练习册系列答案
相关题目