Question

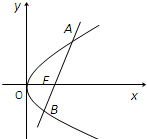
14、直线l经过抛物线y²=4x的焦点，且与抛物线相交于A，B两点，若弦AB中点的横坐标为3，则|AB|=

8

．

Answer 1

分析：线段AB的中点到准线的距离为4，设A，B两点到准线的距离分别为d₁，d₂，由抛物线的定义知|AB|的值．

解答：解：由题设知知线段AB的中点到准线的距离为4，
设A，B两点到准线的距离分别为d₁，d₂，
由抛物线的定义知：
|AB|=|AF|+|BF|=d₁+d₂=2×4=8．
故答案为8．

点评：本题考查抛物线的性质和应用，解题时要认真审题，仔细解答，注意挖掘题设中的隐含条件，积累解题方法．