Question

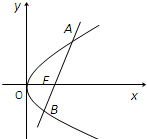
直线l经过抛物线y²=4（x-1）的焦点，且与准线的夹角为30°，则l的方程为

y=±

3

(x-2)

．

Answer 1

分析：先求出抛物线y²=4（x-1）的焦点坐标，再根据与准线的夹角为30°得出直线l的斜率，由点斜式得到直线方程．

解答：解：抛物线y²=4x的焦点为（1，0），
抛物线y²=4（x-1）可看成是由抛物线y²=4x向右平移一个单位得到，其焦点（2，0）．
又直线 l与准线的夹角为30°，则直线l的倾斜角为60°或120°，
其斜率为：±

3

，
故所求直线方程为：y=±

3

（x-2），
故答案为：y=±

3

(x-2)．

点评：本题主要考查直线与圆锥曲线的关系、抛物线的基本性质．属基础题．