题目内容
【题目】定义:![]() 是无穷数列,若存在正整数k使得对任意
是无穷数列,若存在正整数k使得对任意![]() ,均有
,均有![]() 则称
则称![]() 是近似递增(减)数列,其中k叫近似递增(减)数列
是近似递增(减)数列,其中k叫近似递增(减)数列![]() 的间隔数
的间隔数
(1)若![]() ,
,![]() 是不是近似递增数列,并说明理由
是不是近似递增数列,并说明理由
(2)已知数列![]() 的通项公式为
的通项公式为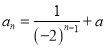 ,其前n项的和为
,其前n项的和为![]() ,若2是近似递增数列
,若2是近似递增数列![]() 的间隔数,求a的取值范围:
的间隔数,求a的取值范围:
(3)已知![]() ,证明
,证明![]() 是近似递减数列,并且4是它的最小间隔数.
是近似递减数列,并且4是它的最小间隔数.
【答案】(1)是近似递增数列,详见解析(2)![]() (3)证明见解析;
(3)证明见解析;
【解析】
(1)根据近似递增数列的定义判断可知![]() 是近似递增数列;
是近似递增数列;
(2)求出![]() ,根据
,根据![]() ,即
,即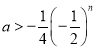 恒成立,可得
恒成立,可得![]() ;
;
(3)因为![]() 等价于
等价于![]() ,因为n,k是正整数,所以
,因为n,k是正整数,所以![]() ,
,![]() 均取不到
均取不到![]() ,所以
,所以![]() 时上式恒成立,可得
时上式恒成立,可得![]() 是近似递减数列,再验证
是近似递减数列,再验证![]() 时,
时,![]() 不是近似递减数列,则可得4是它的最小间隔数.
不是近似递减数列,则可得4是它的最小间隔数.
(1)是近似递增数列,理由如下:
因为![]() ,
,
或![]() [注:2,3,4,…,都是间隔数.]
[注:2,3,4,…,都是间隔数.]
即![]() ,所以
,所以![]() 是近似递增数列.
是近似递增数列.
(2)由题意得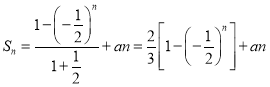 ,
,
所以![]()
![]()
![]()
![]() 对任意
对任意![]() 恒成立,
恒成立,
即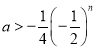 恒成立,.
恒成立,.
令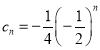 ,则
,则![]() ,
,
即a的取值范围是![]() .
.
(3)因为![]() 等价于
等价于![]() ,
,
即![]() ,(*)
,(*)
因为n,k是正整数,所以![]() ,
,![]() 均取不到
均取不到![]() ,
,
所以![]() 时上式恒成立,即
时上式恒成立,即![]() 是近似递减数列,4是它的间隔数.
是近似递减数列,4是它的间隔数.
当![]() ,当
,当![]() 时,
时,![]() ,故不等式(*)不成立;
,故不等式(*)不成立;
当![]() ,当
,当![]() 时,
时,![]() ,故不等式(*)不成立;
,故不等式(*)不成立;
当![]() ,当
,当![]() 时,
时,![]() ,故不等式(*)不成立;
,故不等式(*)不成立;
所以,4是它的最小间隔数.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目