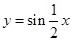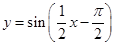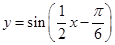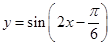题目内容
已知函数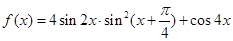 .
.
(Ⅰ)求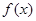 的最小正周期;
的最小正周期;
(Ⅱ)若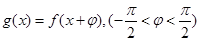 在
在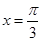 处取得最大值,求
处取得最大值,求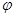 的值;
的值;
(Ⅲ)求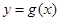 的单调递增区间.
的单调递增区间.
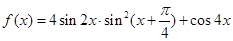 .
.(Ⅰ)求
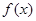 的最小正周期;
的最小正周期;(Ⅱ)若
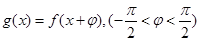 在
在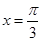 处取得最大值,求
处取得最大值,求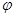 的值;
的值;(Ⅲ)求
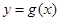 的单调递增区间.
的单调递增区间.(Ⅰ) ;(Ⅱ)
;(Ⅱ) 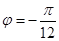 ;(Ⅲ)
;(Ⅲ) 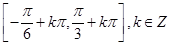 .
.
 ;(Ⅱ)
;(Ⅱ) 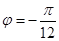 ;(Ⅲ)
;(Ⅲ) 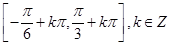 .
.试题分析:(Ⅰ)先根据和角公式以及二倍角公式化简函数:
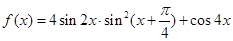 ,得到函数
,得到函数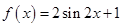 ,再根据
,再根据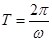 求函数的最小正周期;(Ⅱ)先根据(Ⅰ)中的化简结果求出
求函数的最小正周期;(Ⅱ)先根据(Ⅰ)中的化简结果求出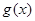 的解析式
的解析式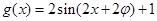 ,然后结合三角函数的图像与性质求得
,然后结合三角函数的图像与性质求得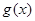 取最大值时对应的
取最大值时对应的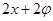 的值,再将
的值,再将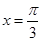 代入求出适合
代入求出适合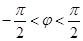 范围内的
范围内的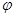 的值;(Ⅲ)根据(Ⅱ)的求解先写出
的值;(Ⅲ)根据(Ⅱ)的求解先写出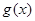 的解析式
的解析式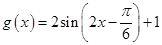 ,结合三角函数的图像与性质得出
,结合三角函数的图像与性质得出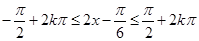 ,解出的
,解出的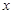 的取值范围即是所求的单调增区间.
的取值范围即是所求的单调增区间.试题解析:(Ⅰ)
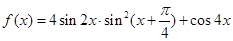
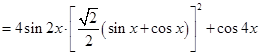
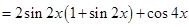
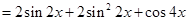
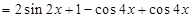
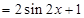 2分
2分所以
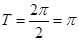 . 4分
. 4分(Ⅱ)
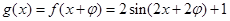 5分
5分当
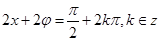 时取得最大值,将
时取得最大值,将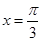 代入上式,
代入上式,解得
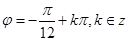 , 6分
, 6分∴
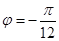 . 8分
. 8分(Ⅲ)由(Ⅱ)知,
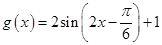 , 9分
, 9分又
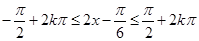 , 10分
, 10分解得
 ,
, ∴函数
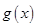 的单调递增区间为:
的单调递增区间为: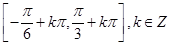 . 12分
. 12分 
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
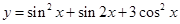 ,求
,求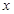 的集合.
的集合. .
. 的最小正周期;
的最小正周期; 上的最大值与最小值.
上的最大值与最小值. .
. 的最小正周期及最小值;
的最小正周期及最小值; ,且
,且 ,求
,求 的值.
的值. 的部分图象如图所示, 为了得到这个函数的图象,只要将
的部分图象如图所示, 为了得到这个函数的图象,只要将 的图象上所有的点 ( )
的图象上所有的点 ( )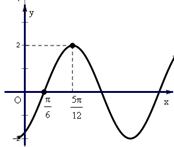
 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变
倍,纵坐标不变 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 的图像与
的图像与 轴的交点的横坐标构成一个公差为
轴的交点的横坐标构成一个公差为 的等差数列,要得到函数
的等差数列,要得到函数 的图像,只需将
的图像,只需将 的图像向右平移____________个单位.
的图像向右平移____________个单位.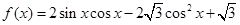 的图象为C:
的图象为C: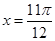 对称; ②函数
对称; ②函数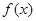 在区间
在区间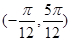 内是增函数;
内是增函数;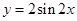 的图象向右平移
的图象向右平移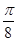 个单位长度可以得到图象C;
个单位长度可以得到图象C;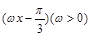 的图象向左平移
的图象向左平移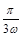 个单位,得到函数y="g" (x)的图象.若y=g(x)在[
个单位,得到函数y="g" (x)的图象.若y=g(x)在[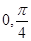 ]上为增函数,则
]上为增函数,则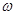 的最大值( )
的最大值( ) 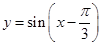 的图象上所有点的横坐标伸长到原来的
的图象上所有点的横坐标伸长到原来的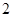 倍(纵坐标不变),再将所得的图象向左平移
倍(纵坐标不变),再将所得的图象向左平移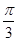 个单位,得到的图象对应的解析式是( )
个单位,得到的图象对应的解析式是( )