题目内容
如图：EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=50°，∠DCF=40°，则∠A的度数是________．
105
分析：做出辅助线，根据四边形一对对角互补，得到四点共圆，根据四点的性质，得到和角A有关的角的度数，根据同弧所对的圆周角等于圆心角的一半，得到结果．
解答：连接OC，OB．
则OB⊥BE，OC⊥EF，
∴O，B，E，C四点共圆，
∵∠E=50°
∴∠BOC=130°．
∠A的度数是
∠BOC+40°=105°
故答案为：105°
点评：本题考查圆周角定理，考查四点共圆的判断和性质，是一个基础题，题目涉及到内容比较少，应用的原理比较简单．
分析：做出辅助线，根据四边形一对对角互补，得到四点共圆，根据四点的性质，得到和角A有关的角的度数，根据同弧所对的圆周角等于圆心角的一半，得到结果．
解答：连接OC，OB．
则OB⊥BE，OC⊥EF，
∴O，B，E，C四点共圆，
∵∠E=50°
∴∠BOC=130°．
∠A的度数是
∠BOC+40°=105°故答案为：105°
点评：本题考查圆周角定理，考查四点共圆的判断和性质，是一个基础题，题目涉及到内容比较少，应用的原理比较简单．
练习册系列答案
相关题目
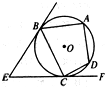如图：EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=50°，∠DCF=40°，则∠A的度数是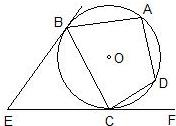
20、如图：EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，则∠A的度数是多少？
如图，EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，则∠A的大小为
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
如图，EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，则∠A的大小为（ ）| A、70° | B、80° | C、90° | D、99° |