题目内容
 如图,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的大小为
如图,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的大小为99°
99°
.分析:连接OB,OC,AC,由EB、EC是⊙O的两条切线,B、C是切点,∠E=46°,∠DCF=32°,得到∠DAC=∠DCF=32°,∠BAC=
(360°-90°-90°-46°)=67°,由此能够求出结果.
| 1 |
| 2 |
解答: 解:如图,连接OB,OC,AC,
解:如图,连接OB,OC,AC,
∵EB、EC是⊙O的两条切线,B、C是切点,
∠E=46°,∠DCF=32°,
∴∠DAC=∠DCF=32°,
∠BAC=
(360°-90°-90°-46°)=67°,
∴∠BAD=32°+67°=99°,
故答案为:99°.
 解:如图,连接OB,OC,AC,
解:如图,连接OB,OC,AC,∵EB、EC是⊙O的两条切线,B、C是切点,
∠E=46°,∠DCF=32°,
∴∠DAC=∠DCF=32°,
∠BAC=
| 1 |
| 2 |
∴∠BAD=32°+67°=99°,
故答案为:99°.
点评:本题考查弦切角的应用,是基础题.解题时要认真审题,仔细解答,注意合理地连接辅助线.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
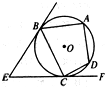 如图,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的大小为( )
如图,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的大小为( )| A、70° | B、80° | C、90° | D、99° |
 如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=50°,∠DCF=40°,则∠A的度数是
如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=50°,∠DCF=40°,则∠A的度数是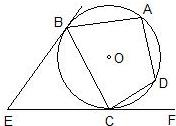 20、如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是多少?
20、如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是多少? (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)