题目内容
设双曲线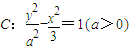 的两条渐近线l1,l2与以点(1,0)为圆心,
的两条渐近线l1,l2与以点(1,0)为圆心, 为半径的圆相切.
为半径的圆相切.(I)求a的值;
(II)若双曲线C的两个焦点分别为F1、F2,A、B分别为l1,l2上的点,且2|AB|=3|F1F2|,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线?
【答案】分析:(I)由题设知:l1,l2的方程为: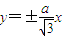 ,由点到直线的距离公式得
,由点到直线的距离公式得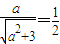 ,由此能求出a的值.
,由此能求出a的值.
(Ⅱ)设A(x1,y1),B(x2,y2),AB的中点M(x,y),由2|AB|=3|F1F2|,知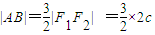 =
= ,再由
,再由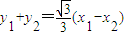 ,
,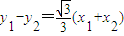 ,能求出线段AB的中点M的轨迹.
,能求出线段AB的中点M的轨迹.
解答:解:(I)由题设知:l1,l2的方程为: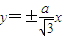 ,
,
由点到直线的距离公式得
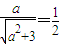 ,
,
∴a=1.
(Ⅱ)设A(x1,y1),B(x2,y2),AB的中点M(x,y),
∵2|AB|=3|F1F2|,
∴
=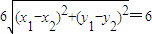 ,
,
又 ,2x=x1+x2,2y=y1+y2,
,2x=x1+x2,2y=y1+y2,
∴ ,
, ,
,
∴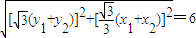 ,
,
∴ ,
,
即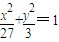 ,
,
所以M的轨迹是中心在原点,焦点在x轴上,长轴长为 ,短轴长为
,短轴长为 的椭圆.
的椭圆.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
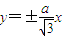 ,由点到直线的距离公式得
,由点到直线的距离公式得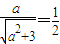 ,由此能求出a的值.
,由此能求出a的值.(Ⅱ)设A(x1,y1),B(x2,y2),AB的中点M(x,y),由2|AB|=3|F1F2|,知
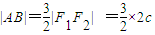 =
= ,再由
,再由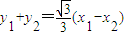 ,
,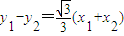 ,能求出线段AB的中点M的轨迹.
,能求出线段AB的中点M的轨迹.解答:解:(I)由题设知:l1,l2的方程为:
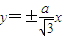 ,
,由点到直线的距离公式得
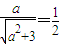 ,
,∴a=1.
(Ⅱ)设A(x1,y1),B(x2,y2),AB的中点M(x,y),
∵2|AB|=3|F1F2|,
∴

=
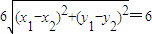 ,
,又
 ,2x=x1+x2,2y=y1+y2,
,2x=x1+x2,2y=y1+y2,∴
 ,
, ,
,∴
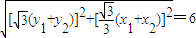 ,
,∴
 ,
,即
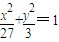 ,
,所以M的轨迹是中心在原点,焦点在x轴上,长轴长为
 ,短轴长为
,短轴长为 的椭圆.
的椭圆.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
设双曲线的两条渐近线为y=±
x=,则该双曲线的离心率e为( )
| 1 |
| 2 |
| A、5 | ||||||
B、
| ||||||
C、
| ||||||
D、
|









 的两条渐近线与直线
的两条渐近线与直线 围成的三角形区域(包括边界)为D,P
围成的三角形区域(包括边界)为D,P 为D内的一个动点,则目标函数
为D内的一个动点,则目标函数 的最小值为( )
的最小值为( ) B.
B. C.0 D.
C.0 D.
 的两条渐近线与直线x=3所围成的三角形区域(包括边界)为E,p(x,y)为该区域内的一动点,则目标函数z=x-
的两条渐近线与直线x=3所围成的三角形区域(包括边界)为E,p(x,y)为该区域内的一动点,则目标函数z=x- 的最小值为( )
的最小值为( )
