题目内容
9.已知等差数列{an}首项为a1,公差为b1,等比数列{bn}首项为b1,公比为a1,其中a1,b1都是大于1的正整数,且a1<b1,b2<a3,对于任意的n∈N*,总存在m∈N*,使得am+5=bn成立,则an=7n-5.分析 an=a1+(n-1)b1,${b}_{n}={b}_{1}{a}_{1}^{n-1}$,根据对于任意的n∈N*,总存在m∈N*,使得am+5=bn成立,可得5+a1+(m-1)b1=${b}_{1}{a}_{1}^{n-1}$,n=1时,可得5+a1=(2-m)b1,由于a1<b1,其中a1,b1都是大于1的正整数,只能m=1,可得5+a1=b1.再根据b2<a3,即可得出.
解答 解:an=a1+(n-1)b1,${b}_{n}={b}_{1}{a}_{1}^{n-1}$,
对于任意的n∈N*,总存在m∈N*,使得am+5=bn成立,
∴5+a1+(m-1)b1=${b}_{1}{a}_{1}^{n-1}$,
n=1时,5+a1+(m-1)b1=b1,∴5+a1=(2-m)b1,
∵a1<b1,其中a1,b1都是大于1的正整数,
∴只能m=1,∴5+a1=b1.∴b1>6.
∵b2<a3,
∴b1a1<a1+2b1,
∴(5+a1)a1<a1+2(5+a1),
化为${a}_{1}^{2}+2{a}_{1}$-10<0,
解得1<a1<$\sqrt{11}$-1,
取a1=2.∴b1=7,an=2+7(n-1)=7n-5;
bn=7×2n-1.
代入am+5=bn,7m-5+5=7×2n-1,化为m=2n-1,满足题意.
故答案为:7n-5.
点评 本题考查了等差数列与等比数列的通项公式、数列的单调性,考查了分析问题与解决问题的能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.用红、黄、蓝、绿4种颜色为一个五棱锥的六个顶点着色,要求每一条棱的两个端点着不同的颜色,则不同的着色方案共有 ( )种?
| A. | 120 | B. | 140 | C. | 180 | D. | 240 |
19.有不少于5个的连续非零自然数的和为2613,则最小的自然数的最大值是( )
| A. | 67 | B. | 78 | C. | 433 | D. | 521 |
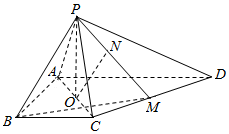 如图,四棱锥P-ABCD,AD∥BC,AD=2BC=4,AB=2$\sqrt{3}$,∠BAD=90°,M,O分别为CD和AC的中点,PO⊥平面ABCD.
如图,四棱锥P-ABCD,AD∥BC,AD=2BC=4,AB=2$\sqrt{3}$,∠BAD=90°,M,O分别为CD和AC的中点,PO⊥平面ABCD.