题目内容
奇函数f（x）在（0，+∞）上为增函数，且f（1）=0，则不等式
＜0的解集为
| f(x) | x |
（-1，0）∪（0，1）
（-1，0）∪（0，1）
．分析：由异号两数相除商为负得到f（x）与x异号，将原等式转化为f（x）x＜0，反映在图象上，即自变量与函数值异号，然后根据条件作出一函数图象，由数形结合法求解．
解答：解：由题意得到f（x）与x异号，
故不等式
＜0可转化为：f（x）x＜0，
即
或
，
根据题意可作函数图象，如右图所示：
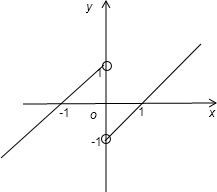由图象可得：当f（x）＞0，x＜0时，-1＜x＜0；
当f（x）＜0，x＞0时，0＜x＜1，
则不等式
＜0的解集是（-1，0）∪（0，1）．
故答案为：（-1，0）∪（0，1）
故不等式
| f(x) |
| x |
即
|
|
根据题意可作函数图象，如右图所示：
由图象可得：当f（x）＞0，x＜0时，-1＜x＜0；当f（x）＜0，x＞0时，0＜x＜1，
则不等式
| f(x) |
| x |
故答案为：（-1，0）∪（0，1）
点评：此题考查了其他不等式的解法，以及奇偶性与单调性的综合，利用了数形结合及转化的思想，灵活运用数形结合的思想方法是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
定义在（-∞，0）∪（0，+∞）上的奇函数f（x）在（0，+∞）上为增函数，当x＞0时，f（x）的图象如图所示，则不等式x[f（x）-f（-x）]＜0的解集是（ ）