题目内容
(本题满分16分,第(1)小题8分,第(2)小题8分)
己知双曲线的中心在原点,右顶点为
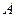 (1,0),点
(1,0),点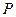 、Q在双曲线的右支上,点
、Q在双曲线的右支上,点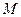 (
(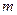 ,0)到直线
,0)到直线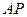 的距离为1.
的距离为1.
(1)若直线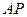 的斜率为
的斜率为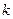 且有
且有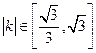 ,求实数
,求实数 的取值范围;
的取值范围;
(2)当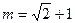 时,
时,
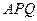 的内心恰好是点
的内心恰好是点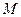 ,求此双曲线的方程.
,求此双曲线的方程.
己知双曲线的中心在原点,右顶点为

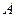 (1,0),点
(1,0),点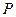 、Q在双曲线的右支上,点
、Q在双曲线的右支上,点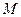 (
(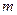 ,0)到直线
,0)到直线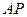 的距离为1.
的距离为1.(1)若直线
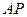 的斜率为
的斜率为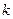 且有
且有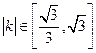 ,求实数
,求实数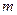 的取值范围;
的取值范围;(2)当
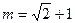 时,
时,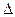
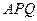 的内心恰好是点
的内心恰好是点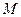 ,求此双曲线的方程.
,求此双曲线的方程.(Ⅰ)  或
或 ; (Ⅱ)
; (Ⅱ) 
 或
或 ; (Ⅱ)
; (Ⅱ) 
设直线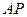 的方程为:
的方程为: ,…………………2分
,…………………2分
由点 到直线
到直线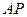 的距离为
的距离为 可知:
可知:
 得到
得到 ,…………………5分
,…………………5分
因为 ,所以
,所以
 ,
,
所以 ,
, 或
或
所以 或
或 ;…………………8分
;…………………8分
(2)当 时,
时, ,
,
由于点 到直线
到直线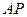 的距离为
的距离为 ,所以直线
,所以直线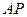 的斜率
的斜率 ,……10分
,……10分
因为点 为
为 的内心,故
的内心,故 是双曲线上关于
是双曲线上关于 轴对称的两点,所以
轴对称的两点,所以 轴,不妨设直线
轴,不妨设直线 交
交 轴于点
轴于点 ,则
,则 ,
,
所以点 的坐标为
的坐标为 ,…………………12分
,…………………12分
所以 两点的横坐标均为
两点的横坐标均为 ,把
,把 代入直线
代入直线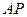 的方程:
的方程: ,得
,得 ,所以
,所以 两点的坐标分别为:
两点的坐标分别为: ,
,
设双曲线方程为: ,把点
,把点 的坐标代入方程得到
的坐标代入方程得到
 ,…………………15分
,…………………15分
所以双曲线方程为: …………………16分
…………………16分
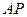 的方程为:
的方程为: ,…………………2分
,…………………2分由点
 到直线
到直线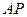 的距离为
的距离为 可知:
可知: 得到
得到 ,…………………5分
,…………………5分因为
 ,所以
,所以
 ,
,所以
 ,
, 或
或
所以
 或
或 ;…………………8分
;…………………8分(2)当
 时,
时, ,
,由于点
 到直线
到直线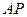 的距离为
的距离为 ,所以直线
,所以直线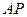 的斜率
的斜率 ,……10分
,……10分因为点
 为
为 的内心,故
的内心,故 是双曲线上关于
是双曲线上关于 轴对称的两点,所以
轴对称的两点,所以 轴,不妨设直线
轴,不妨设直线 交
交 轴于点
轴于点 ,则
,则 ,
,所以点
 的坐标为
的坐标为 ,…………………12分
,…………………12分所以
 两点的横坐标均为
两点的横坐标均为 ,把
,把 代入直线
代入直线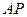 的方程:
的方程: ,得
,得 ,所以
,所以 两点的坐标分别为:
两点的坐标分别为: ,
, 设双曲线方程为:
 ,把点
,把点 的坐标代入方程得到
的坐标代入方程得到 ,…………………15分
,…………………15分所以双曲线方程为:
 …………………16分
…………………16分
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
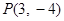 是双曲线
是双曲线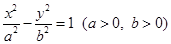 渐近线上的一点,
渐近线上的一点,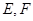 是左、右两个焦点,若
是左、右两个焦点,若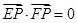 ,则双曲线方程为
,则双曲线方程为 
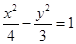
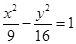
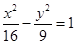
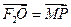 ,
,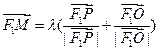
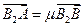 ,求
,求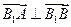 时,直线AB的方程.
时,直线AB的方程.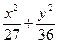 =1有共同的焦点,且与此椭圆一个交点的纵坐标为4,求这个双曲线的方程.
=1有共同的焦点,且与此椭圆一个交点的纵坐标为4,求这个双曲线的方程. -
- =1的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离是__________________.
=1的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离是__________________.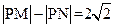 ,该动点的轨迹为F,
,该动点的轨迹为F,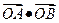 的最小值。
的最小值。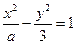 上的一条渐近线方程为
上的一条渐近线方程为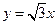 ,则抛物线
,则抛物线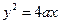 上一点
上一点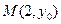 到该抛物线焦点
到该抛物线焦点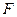 的距离是 。
的距离是 。