题目内容
已知抛物线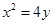 ,直线
,直线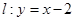 ,
,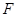 是抛物线的焦点。
是抛物线的焦点。
(1)在抛物线上求一点 ,使点
,使点 到直线
到直线 的距离最小;
的距离最小;
(2)如图,过点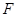 作直线交抛物线于A、B两点.
作直线交抛物线于A、B两点.
①若直线AB的倾斜角为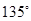 ,求弦AB的长度;
,求弦AB的长度;
②若直线AO、BO分别交直线 于
于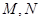 两点,求
两点,求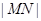 的最小值.
的最小值.
(1)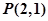 ;(2)①
;(2)① ;②
;②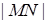 的最小值是
的最小值是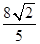 .
.
解析试题分析:(1)数形结合,找出与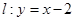 与平行的切线的切点即为P.(2)易得直线方程
与平行的切线的切点即为P.(2)易得直线方程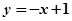 ,与抛物线联立,利用弦长公式,可求AB;②设
,与抛物线联立,利用弦长公式,可求AB;②设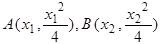 ,可得AO,BO方程,与抛物线联立
,可得AO,BO方程,与抛物线联立
试题解析:
解:(1)设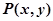 ,
,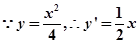 ,
,
由题可知: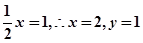
所求的点为: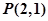 (或者用距离公式或
(或者用距离公式或 同样给分) 3分
同样给分) 3分
(2)①易知直线AB: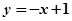 ,
,
联立: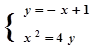 ,消去y得,
,消去y得,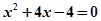 5分
5分
设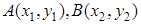 ,则
,则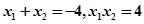
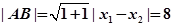 (用定义同样给分) 8分
(用定义同样给分) 8分
②设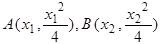 ,所以
,所以
所以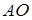 的方程是:
的方程是: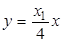 ,由
,由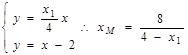 ,
,
同理由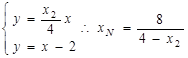 9分
9分
所以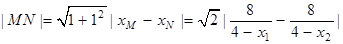
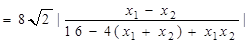 ① 10分
① 10分
设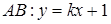 ,由
,由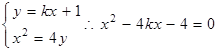 ,
,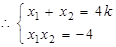 且
且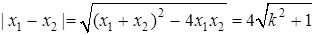 ,
,
代入①得到: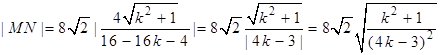 , 12分
, 12分
设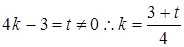 ,
,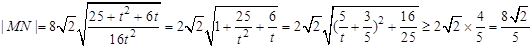 ,
,
所以此时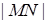 的最小值是
的最小值是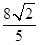 ,此时
,此时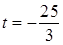 ,
,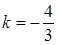 ; 13分
; 13分
综上: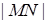 的最小值是
的最小值是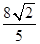 。 14分
。 14分
考点:抛物线的几何性质,弦长公式,数形结合的数学思想.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
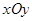 中,已知动点
中,已知动点 到点
到点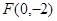 的距离为
的距离为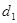 ,到
,到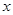 轴的距离为
轴的距离为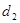 ,且
,且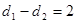 .
.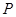 的轨迹
的轨迹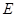 的方程;
的方程;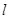 斜率为1且过点
斜率为1且过点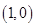 ,其与轨迹
,其与轨迹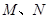 ,求
,求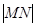 的值.
的值.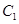 :
: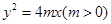 的准线与
的准线与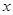 轴交于点
轴交于点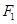 ,焦点为
,焦点为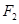 ;椭圆
;椭圆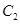 以
以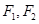 为焦点,离心率
为焦点,离心率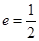 .设
.设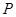 是
是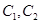 的一个交点.
的一个交点.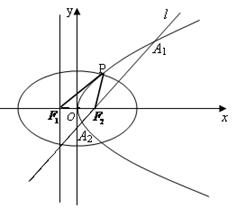
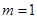 时,求椭圆
时,求椭圆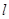 过
过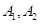 两点,且
两点,且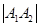 等于
等于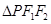 的周长,求
的周长,求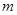 ,使得
,使得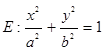 (a>b>0)的离心率为
(a>b>0)的离心率为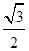 ,且过点(
,且过点(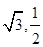 ).
).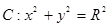 (1<R<2)相切于点A,且l与椭圆E只有一个公共点B.
(1<R<2)相切于点A,且l与椭圆E只有一个公共点B.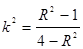 ;
;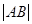 取得最大值?并求出最大值.
取得最大值?并求出最大值.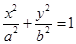 (a>b>0)的离心率为
(a>b>0)的离心率为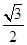 ,过其右焦点F与长轴垂直的弦长为1,
,过其右焦点F与长轴垂直的弦长为1,
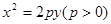 的焦点为
的焦点为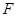 ,点
,点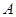 为抛物线上的一点,其纵坐标为
为抛物线上的一点,其纵坐标为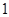 ,
,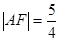 .
.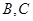 为抛物线上不同于
为抛物线上不同于 ,过
,过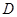 ,求
,求 的最小值.
的最小值. 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合. 的值.
的值. 交椭圆
交椭圆 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆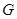 :
: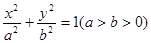 的离心率为
的离心率为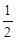 ,过椭圆
,过椭圆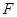 的直线
的直线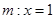 与椭圆
与椭圆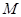 (点
(点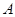 为椭圆
为椭圆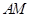 的直线
的直线 与椭圆相交于
与椭圆相交于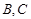 两点.判断直线
两点.判断直线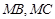 是否关于直线
是否关于直线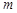 对称,并说明理由.
对称,并说明理由.