题目内容
(本小题满分12分)
若函数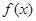 为奇函数,当
为奇函数,当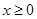 时,
时,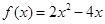 (如图).
(如图).
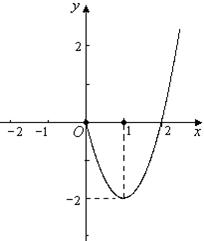
(Ⅰ)求函数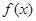 的表达式,并补齐函数
的表达式,并补齐函数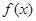 的图象;
的图象;
(Ⅱ)用定义证明:函数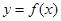 在区间
在区间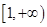 上单调递增.
上单调递增.
若函数
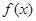 为奇函数,当
为奇函数,当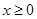 时,
时,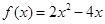 (如图).
(如图).
(Ⅰ)求函数
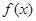 的表达式,并补齐函数
的表达式,并补齐函数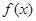 的图象;
的图象;(Ⅱ)用定义证明:函数
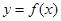 在区间
在区间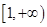 上单调递增.
上单调递增.(1)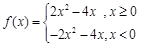 (2)利用定义法,设变量,作差,变形,定号,下结论。
(2)利用定义法,设变量,作差,变形,定号,下结论。
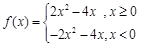 (2)利用定义法,设变量,作差,变形,定号,下结论。
(2)利用定义法,设变量,作差,变形,定号,下结论。试题分析:解:(Ⅰ)
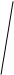 任取
任取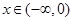 ,则
,则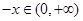 由
由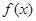 为奇函数,
为奇函数,则
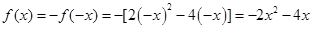 ………………………4分
………………………4分综上所述,
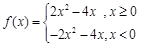 …………………………………………5分
…………………………………………5分补齐图象。(略)…………………………………………6分
(Ⅱ)任取
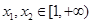 ,且
,且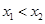 ,…………………………………7分
,…………………………………7分则
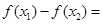
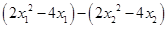 ………………………………8分
………………………………8分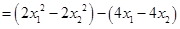
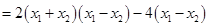
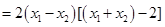 …………………………………10分
…………………………………10分∵
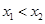 ∴
∴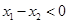
又由
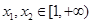 ,且
,且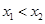 ,所以
,所以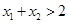 ,∴
,∴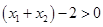
∴
 ,
,∴
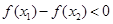 ,即
,即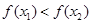 ………………………………………11分
………………………………………11分∴函数
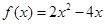 在区间
在区间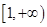 上单调递增。…………………………12分
上单调递增。…………………………12分点评:解决该试题利用奇函数关于原点的对称性求解函数图像,同时能利用单调性的定义法证明单调性。属于基础题。

练习册系列答案
相关题目
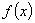 和偶函数
和偶函数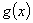 满足
满足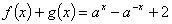
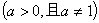 ,若
,若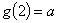 ,则
,则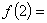
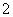
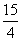
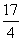
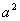
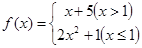 ,则
,则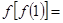 .
.  平方米.
平方米.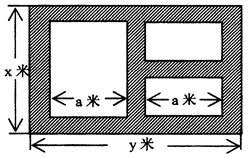
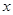 表示
表示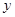 和用
和用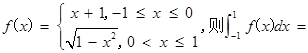 ( )
( )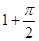
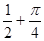
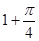
 在区间
在区间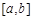 上是减函数,则
上是减函数,则 上是
上是

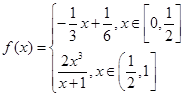 ,函数
,函数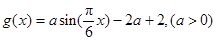 ,若存在
,若存在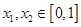 ,使得
,使得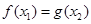 成立,则实数
成立,则实数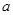 的取值范围是 。
的取值范围是 。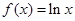 ,
,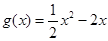 .
.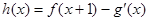 (其中
(其中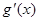 是
是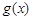 的导函数),求
的导函数),求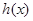 的最大值;
的最大值;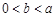 时,有
时,有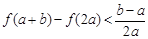 ;
;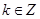 ,当
,当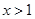 时,不等式
时,不等式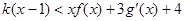 恒成立,求
恒成立,求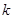 的最大值.
的最大值.