题目内容
如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ,每一次游戏得到奖励分为ξ(1)求x<2且y>1的概率;
(2)某人进行了12次游戏,求他平均可以得到的奖励分.

【答案】分析:(1)在两个图中三个扇形区域的圆心角分别为60°、120°、180°,根据圆心角度数,求出x和y取不同值时的概率,根据互斥事件的概率求出结论.
(2)由条件可知ξ的取值为:2、3、4、5、6,当ξ=2时,即x=1且y=1,根据独立事件同时发生的概率做出结果,用同样的方法可以求出其他值对应的概率,写出分布列和期望,估计平均可以得到的奖励分.
解答:解:(1)由几何概率模型可知:
 ;
;

∴ ,
,
∴
(2)由条件可知ξ的取值为:2、3、4、5、6,
当ξ=2时,即x=1且y=1,P(ξ=2)=P(x=1)P(y=1)= ,
,
用同样的方法可以求出其他值对应的概率
P(ξ=3)= ,P(ξ=4)=
,P(ξ=4)= ,P(ξ=5)=
,P(ξ=5)= ,P(ξ=6)=
,P(ξ=6)=
∴ξ的分布列为:
他平均一次得到的奖励分即为ξ的期望值: .
.
∴给他玩12次平均可以得到12•Eξ=50
点评:考查运用概率知识解决实际问题的能力,注意满足独立重复试验的条件,解题过程中判断概率的类型是难点也是重点,这种题目高考必考,应注意解题的格式.
(2)由条件可知ξ的取值为:2、3、4、5、6,当ξ=2时,即x=1且y=1,根据独立事件同时发生的概率做出结果,用同样的方法可以求出其他值对应的概率,写出分布列和期望,估计平均可以得到的奖励分.
解答:解:(1)由几何概率模型可知:
 ;
;
∴
 ,
,∴

(2)由条件可知ξ的取值为:2、3、4、5、6,
当ξ=2时,即x=1且y=1,P(ξ=2)=P(x=1)P(y=1)=
 ,
,用同样的方法可以求出其他值对应的概率
P(ξ=3)=
 ,P(ξ=4)=
,P(ξ=4)= ,P(ξ=5)=
,P(ξ=5)= ,P(ξ=6)=
,P(ξ=6)=
∴ξ的分布列为:
| ξ | 2 | 3 | 4 | 5 | 6 |
| P |  |  |  |  |  |
 .
.∴给他玩12次平均可以得到12•Eξ=50
点评:考查运用概率知识解决实际问题的能力,注意满足独立重复试验的条件,解题过程中判断概率的类型是难点也是重点,这种题目高考必考,应注意解题的格式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
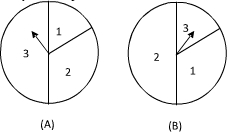 如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ,每一次游戏得到奖励分为ξ
如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ,每一次游戏得到奖励分为ξ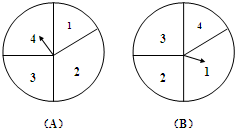 (2010•珠海二模)如图是两个独立的转盘(A)、(B),在两个图中的四个扇形区域的圆心角分别为60°、120°、90°90°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域数为y,x、y∈{1,2,3,4},设x+y的值为ξ,每一次游戏得到奖励分为ξ.
(2010•珠海二模)如图是两个独立的转盘(A)、(B),在两个图中的四个扇形区域的圆心角分别为60°、120°、90°90°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域数为y,x、y∈{1,2,3,4},设x+y的值为ξ,每一次游戏得到奖励分为ξ.
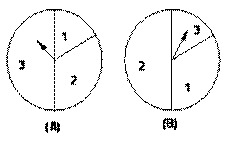
 ,用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,
,用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,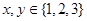 ,设
,设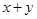 的值为
的值为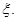
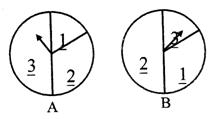
 的概率;
的概率; 的发布列与数学期望。
的发布列与数学期望。