题目内容
10．
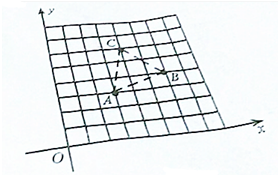如图，A、B、C为一个平行四边形的三个顶点，且A、B、C三点的坐标分别为（3，3）、（6，4）、（4，6）．（1）请直接写出这个平行四边形的第四个顶点的坐标；
（2）求这个平行四边形的面积．
分析 （1）利用平行四边形的性质，直接写出这个平行四边形的第四个顶点的坐标；
（2）利用平行四边形的面积都是三角形的面积的2倍，求解即可．
解答 解：（1）由平行四边形的平行性质，可知这个平行四边形的第四个顶点的坐标可以为（7，7）或（5，1）或（1，5）；
（2）这个平行四边形的面积都是三角形ABC面积的2倍，三角形的面积为：$\frac{1}{2}×4×3-\frac{1}{2}×4×1$=4．
所以平行四边形的面积为8．
点评 本题考查向量的平面几何中的应用，向量的坐标运算，注意平行四边形的特征是解题的关键．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
2．下列命题为真命题的是（ ）
| A． | 已知a，b∈R，则“$\frac{{{a^2}+{b^2}}}{ab}≤-2$”是“a＞0且b＜0”的充分不必要条件 | |
| B． | 已知数列{an}为等比数列，则“a1＜a2＜a3”是“a4＜a5”的既不充分也不必要条件 | |
| C． | 已知两个平面α，β，若两条异面直线m，n满足m?α，n?β且m∥β，n∥α，则α∥β | |
| D． | ?x0∈（-∞，0），使${3^{x_0}}＜{4^{x_0}}$成立 |