题目内容
20．化简：$\frac{cos（\frac{π}{2}+α）•cos（2π-α）•sin（-α+\frac{3π}{2}）}{sin（-π-α）•sin（\frac{3π}{2}+α）}$．分析 运用诱导公式即可化简．
解答 解：$\frac{cos（\frac{π}{2}+α）•cos（2π-α）•sin（-α+\frac{3π}{2}）}{sin（-π-α）•sin（\frac{3π}{2}+α）}$=$\frac{（-sinα）•cosα•（-cosα）}{sinα•（-cosα）}$=-cosα．
点评 本题主要考查了诱导公式在化简求值中的应用，属于基本知识的考查．
练习册系列答案
相关题目
5．
在如图所示的坐标平面的可行域内（阴影部分且包括边界），若目标函数z=x+ay取得最小值的最优解有无数个，则$\frac{y}{x-a}$的最大值是（ ）
在如图所示的坐标平面的可行域内（阴影部分且包括边界），若目标函数z=x+ay取得最小值的最优解有无数个，则$\frac{y}{x-a}$的最大值是（ ）| A． | $\frac{2}{7}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{4}$ |
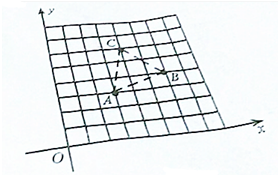如图，A、B、C为一个平行四边形的三个顶点，且A、B、C三点的坐标分别为（3，3）、（6，4）、（4，6）．