Question

【题目】已知是公差不为零的等差数列，满足，且、、成等比数列.

（1）求数列的通项公式；

（2）设数列满足，求数列的前项和.

【答案】（1）；（2）

【解析】试题分析：（1）设等差数列 的公差为，由a3=7，且、、成等比数列．可得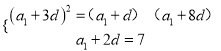，解之得即可得出数列的通项公式；

2）由（1）得，则，由裂项相消法可求数列的前项和.

试题解析：（1）设数列的公差为，且由题意得，

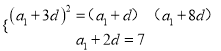即 ，解得，

所以数列的通项公式.

（2）由（1）得

，

.

【题型】解答题
【结束】
18

【题目】四棱锥的底面为直角梯形，，，，为正三角形.

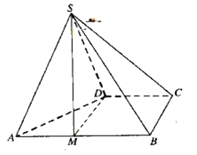
（1）点为棱上一点，若平面，，求实数的值；

（2）求点B到平面SAD的距离.

Answer 1

【答案】（1）；（2）

【解析】试题分析：（1）由平面，可证，进而证得四边形为平行四边形，根据，可得；

（2）利用等体积法可求点到平面的距离.

试题解析：（（1）因为平面SDM，

平面ABCD，

平面SDM 平面ABCD=DM，

所以，

因为，所以四边形BCDM为平行四边形，又，所以M为AB的中点.

因为，

.

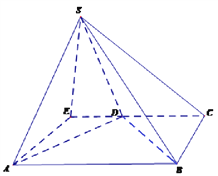
（2）因为 ， ，

所以平面，

又因为平面，

所以平面平面，

平面平面，

在平面内过点作直线于点，则平面，

在和中，

因为，所以，

又由题知，

所以，

由已知求得，所以，

连接BD，则，

又求得的面积为，

所以由点B 到平面的距离为.