题目内容
6.若a=$\frac{1}{\sqrt{2}}$,b=$\frac{1}{\root{3}{2}}$,则[${a}^{-\frac{3}{2}}{b}^{2}(a{b}^{-2})^{-\frac{1}{2}}$]2=1.分析 先利用分数指数幂的性质和运算法则把[${a}^{-\frac{3}{2}}{b}^{2}(a{b}^{-2})^{-\frac{1}{2}}$]2化简为a-4b6,再把a=$\frac{1}{\sqrt{2}}$,b=$\frac{1}{\root{3}{2}}$代入,能求出结果.
解答 解:∵a=$\frac{1}{\sqrt{2}}$,b=$\frac{1}{\root{3}{2}}$,
∴[${a}^{-\frac{3}{2}}{b}^{2}(a{b}^{-2})^{-\frac{1}{2}}$]2=a-3b4a-1b2=a-4b6
=($\frac{1}{\sqrt{2}}$)-4($\frac{1}{\root{3}{2}}$)6
=$({2}^{-\frac{1}{2}})^{-4}$•$({2}^{-\frac{1}{3}})^{6}$
=22•2-2
=1.
故答案为:1.
点评 本题考查有理数指数幂的化简求值,是基础题,解题时要认真审题,注意有理数指数幂的性质和运算法则的合理运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
11.若f(x)的定义域为[-3,1],则函数F(x)=f(x)+f(-x)的定义域为( )
| A. | [-3,3] | B. | [-1,1] | C. | [-3,1] | D. | [-1,3] |
15.函数y=$\frac{\sqrt{x+3}}{4-{x}^{2}}$的定义域为( )
| A. | [-3,-2)∪(-2,2) | B. | [-3,-2)∪(2,+∞) | C. | [-3,-2)∪(-2,2) | D. | [-3,-2)∪(-2,2)∪(2,+∞) |
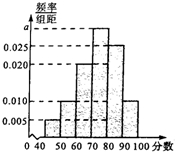 某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.