Question

已知函数y=(k²+4k-5)x²+4(1-k)x+3对于任意的实数x函数值恒大于0，求k的取值范围.

Answer 1

解：(1)当k²+4k-5=0时，k=-5或k=1.

若k=-5,则y=24x+3,对任意实数x，函数值不恒大于0.

若k=1,则y=3,对任意实数x，函数值恒大于0.

(2)当k²+4k-5≠0时，

∵函数y=(k²+4k-5)x²+4(1-k)x+3对于任意的实数x函数值恒大于0，

∴

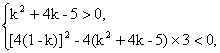
即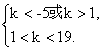

∴1＜k＜19.

实数k的取值范围为1≤k＜19.