题目内容
已知数列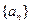 的首项
的首项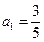 ,
,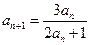 ,
,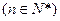 .
.
(1)求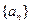 的通项公式;
的通项公式;
(2)证明:对任意的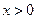 ,
,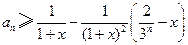 ,
,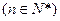 ;
;
(3)证明: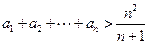 .
.
(1)解: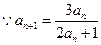 ,
,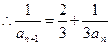 ,
,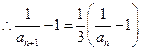 ,
,
又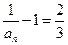 ,
,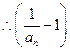 是以
是以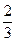 为首项,
为首项,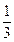 为公比的等比数列.
为公比的等比数列.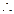
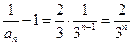 ,
,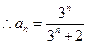 .
.
(2)证法一:由(1)知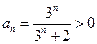 ,
,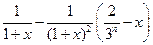
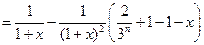
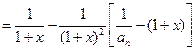
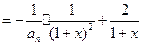
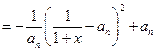
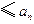 ,
,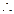 原不等式成立.
原不等式成立.
证法二:设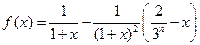 ,
,
则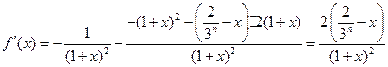
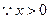 ,
,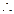 当
当 时,
时,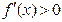 ;当
;当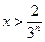 时,
时,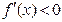 ,
,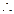 当
当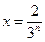 时,
时,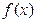 取得最大值
取得最大值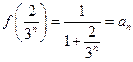 .
.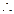 原不等式成立.
原不等式成立.
(3)证明:由(2)知,对任意的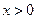 ,有
,有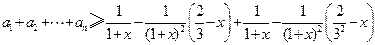
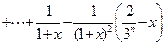
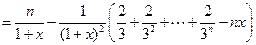 .
.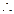 取
取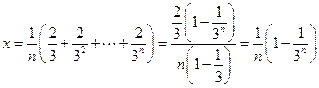 ,
,
则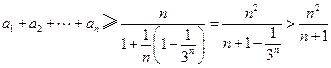 .
.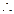 原不等式成立.
原不等式成立.
解析

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知数列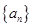 的首项
的首项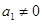 ,其前
,其前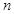 项的和为
项的和为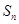 ,且
,且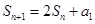 ,则
,则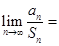
| A.0 | B.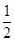 | C.1 | D.2 |
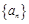 的首项为
的首项为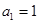 ,且
,且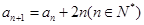 ,则这个数列的通项公式为___________
,则这个数列的通项公式为___________