题目内容
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 上不单调,求实数a的取值范围;
上不单调,求实数a的取值范围;
(2)求函数![]() 在
在![]() 的最小值.
的最小值.
【答案】(1)![]()
(2)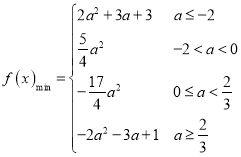 .
.
【解析】
(1)分![]() 与
与![]() 两种情况将
两种情况将![]() 写成分段函数的形式,再根据对称轴与区间
写成分段函数的形式,再根据对称轴与区间![]() 的位置关系讨论即可
的位置关系讨论即可
(2)先分![]() ,
,![]() 两种情况讨论,再根据两个二次函数的对称轴再对
两种情况讨论,再根据两个二次函数的对称轴再对![]() 进行讨论分析最小值的取值情况.
进行讨论分析最小值的取值情况.
(1)由![]() 化为
化为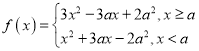
则二次函数![]() 对称轴为
对称轴为![]() .
.
![]() 对称轴为
对称轴为![]()
则当![]() 时, 若函数
时, 若函数![]() 在
在![]() 上不单调则对称轴
上不单调则对称轴![]() 在
在![]() 之间,
之间,
即![]() ,因为
,因为![]() 故化简得
故化简得![]() ,即
,即![]()
当![]() 时,
时, 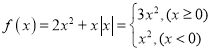 满足题意.
满足题意.
当![]() 时, 若函数
时, 若函数![]() 在
在![]() 上不单调则对称轴
上不单调则对称轴![]() 在
在![]() 之间,
之间,
即![]() ,因为
,因为![]() 故
故![]()
综上所述, ![]()
(2) 由(1) 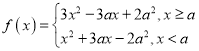 ,
,![]()
![]() 对称轴为
对称轴为![]() .
.
![]() 对称轴为
对称轴为![]()
1.当![]() 时,
时,
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
此时![]()
当![]() 即
即![]() 时,
时, ![]() 在
在![]() 的对称轴
的对称轴![]() 处取得最小值,
处取得最小值,
此时![]()
2.当![]() 时,
时,
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
此时![]()
当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 的对称轴
的对称轴![]() 处取得最小值,
处取得最小值,
此时![]()
综上所述,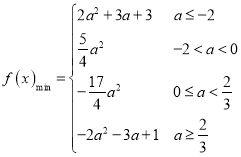

练习册系列答案
相关题目
【题目】某企业生产![]() 、
、![]() 两种产品,生产每
两种产品,生产每![]() 产品所需的劳动力和煤、电消耗如下表:
产品所需的劳动力和煤、电消耗如下表:
产品品种 | 劳动力(个) | 煤 | 电 |
|
|
|
|
|
|
|
|
已知生产![]() 产品的利润是
产品的利润是![]() 万元,生产
万元,生产![]() 产品的利润是
产品的利润是![]() 万元.现因条件限制,企业仅有劳动力
万元.现因条件限制,企业仅有劳动力![]() 个,煤
个,煤![]() ,并且供电局只能供电
,并且供电局只能供电![]() ,则企业生产
,则企业生产![]() 、
、![]() 两种产品各多少吨,才能获得最大利润?
两种产品各多少吨,才能获得最大利润?