题目内容
设集合M={x|a1x2+b1x+c1=0},N={x|a2x2+b2x+c2=0},方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集一定是
- A.M∩N
- B.M∪N
- C.M
- D.N
B
分析:先将方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集转化为满足a1x2+b1x+c1=0或a2x2+b2x+c2=0,也即集合M={x|a1x2+b1x+c1=0},集合N={a2x2+b2x+c2=0}的并集,从而得出方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集的表示法.
解答:方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集转化为:
满足a1x2+b1x+c1=0或a2x2+b2x+c2=0,
也即集合M={x|a1x2+b1x+c1=0},集合N={a2x2+b2x+c2=0}的并集,
从而得出方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集可用M、N表示为M∪N.
故选B.
点评:本小题主要考查交、并、补集的混合运算、方程式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
分析:先将方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集转化为满足a1x2+b1x+c1=0或a2x2+b2x+c2=0,也即集合M={x|a1x2+b1x+c1=0},集合N={a2x2+b2x+c2=0}的并集,从而得出方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集的表示法.
解答:方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集转化为:
满足a1x2+b1x+c1=0或a2x2+b2x+c2=0,
也即集合M={x|a1x2+b1x+c1=0},集合N={a2x2+b2x+c2=0}的并集,
从而得出方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集可用M、N表示为M∪N.
故选B.
点评:本小题主要考查交、并、补集的混合运算、方程式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目

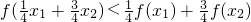 成立,则f(x)是定义在D上的β函数.
成立,则f(x)是定义在D上的β函数.