题目内容
如图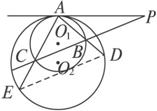
图
证明:连结DE,∵∠PAB=∠ACB,∠P=∠P,
∴△PAB∽△PCA.∴![]() =
=![]() .
.
∵∠PAD=∠E,∠PAB=∠ACB,
∴∠ACB=∠E.同理,∠ABC=∠D.
∴BC∥DE.∴![]() =
=![]() .
.
∴![]() =
=![]() .∴
.∴![]() =
=![]() .
.
又由切割线定理,得PA2=PB·PC,
∴![]() .∴
.∴![]() .
.

练习册系列答案
相关题目
 对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.
对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.(1)根据图中的数据,制作2×2列表;
(2)若要从更爱好文娱和从更爱好体育的学生中各选一人分别作文体活动的协调人,求选出的两人恰好是一男一女的概率;
(3)在多大的程度上可以认为性别与是否爱好体育有关系?
参考数据:
| P(K2≥k) | 0.5 | 0.4 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
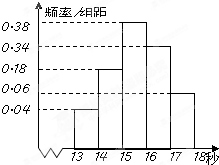 (2011•西山区模拟)为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(2011•西山区模拟)为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图. 某市在“节约用水、保护水资源”的宣传教育活动中发布两则公益广告,活动组织者为了了解宣传效果,对10~60岁人群随机抽样调查了n人,要求被调查人回答两则广告的内容,调查结果如下表所示:
某市在“节约用水、保护水资源”的宣传教育活动中发布两则公益广告,活动组织者为了了解宣传效果,对10~60岁人群随机抽样调查了n人,要求被调查人回答两则广告的内容,调查结果如下表所示: 某大学高等数学老师上学期分别采用了A,B两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如图:
某大学高等数学老师上学期分别采用了A,B两种不同的教学方式对甲、乙两个大一新生班进行教改试验(两个班人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩,得到茎叶图如图: