题目内容
已知椭圆C的两焦点分别为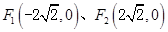
，长轴长为6，
⑴求椭圆C的标准方程;
⑵已知过点（0，2）且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度。.
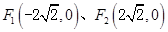，长轴长为6，⑴求椭圆C的标准方程;
⑵已知过点（0，2）且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度。.
（1）
；（2）
；（2）试题分析：（1）由焦点坐标可得
的值，由长轴长可得
的值，再根据椭圆中
，求
。从而可得椭圆方程。（2）由点斜式可得直线方程为
。将直线方程与椭圆方程联立消去
得关于
的一元二次方程，可得根与系数的关系。再根据弦长公式求线段
的长。⑴由
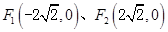，长轴长为6 得：
所以
∴椭圆方程为
5分⑵设
,由⑴可知椭圆方程为①,∵直线AB的方程为
② 7分把②代入①得化简并整理得
∴
10分又
12分
练习册系列答案
阅读快车系列答案
相关题目
，长轴长为6，
，椭圆
的方程为
，双曲线
的方程为
，
，则
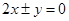
的左右焦点分别为
，若椭圆C上恰好有6个不同的点
，使得
为等腰三角形，则椭圆C的离心率取值范围是（ ）
的离心率为
，点
在椭圆上.
的动直线与椭圆交于M，N两点，连接AN、BM相交于G点，试求点G的横坐标的值.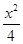
＋y2＝1，F1，F2为其两焦点，P为椭圆上任一点．则|PF1|·|PF2|的最大值为( )
的焦点与椭圆
的左焦点重合，则
的值为（ ）
的左、右焦点，A为双曲线的左顶点，以F1F2为直径的圆交双曲线的某条渐近线于M、N两点，且满足
MAN=120o，则该双曲线的离心率为( )
中，椭圆
的中心为原点，焦点
在
轴上，离心率为
。过
的直线L交C于
两点，且
的周长为16，那么