题目内容
已知椭圆C的两焦点分别为
，长轴长为6，
⑴求椭圆C的标准方程;
⑵已知过点（0，2）且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度。．
，长轴长为6，⑴求椭圆C的标准方程;
⑵已知过点（0，2）且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度。．
⑴
；⑵
．
；⑵．试题分析：⑴两焦点间距离为
，由焦点坐标可得
值，椭圆长轴长为
，由长轴长为
，得
，由椭圆中
，可得
值，可求得椭圆的标准方程；⑵由条件可得直线
的方程为
，设
，将直线方程与椭圆方程联立方程组，可化为
，则可得
，由弦长公式
，可得．解：⑴由
，长轴长为6 ，得：
所以
， ∴椭圆方程为
⑵设
,由⑴可知椭圆方程为
①,∵直线AB的方程为
② 把②代入①得化简并整理得
,∴
又
练习册系列答案
全能练考卷系列答案
相关题目
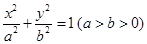过点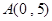
，
，C、D在该椭圆上，直线CD过原点O，且在线段AB的右下侧．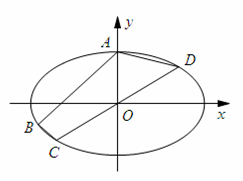
的焦点在
轴上, 
分别是椭圆的左、右焦点，点
是椭圆在第一象限内的点，直线
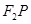交
轴于点
，
时，
的离心率为
，求椭圆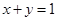
上时，求直线
与
的夹角;
时，若总有
，猜想:当
变化时，点
是否在某定直线上，若是写出该直线方程（不必求解过程）．
，
＝2
，则C的离心率为________．
的离心率是
，则
的值为 .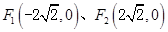
，长轴长为6，