题目内容
(12分) 已知圆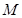 过两点
过两点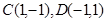 ,且圆心
,且圆心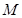 在
在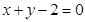 上.
上.
(1)求圆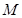 的方程;
的方程;
(2)设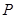 是直线
是直线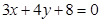 上的动点,
上的动点,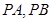 是圆
是圆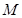 的两条切线,
的两条切线,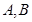 为切点,求四边形
为切点,求四边形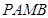 面积的最小值.
面积的最小值.
【答案】
(1) 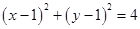 (2) 2
(2) 2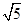
【解析】
试题分析:(1)设圆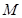 的方程为:(x-a)2+(y-b)2=r2(r>0).
的方程为:(x-a)2+(y-b)2=r2(r>0).
根据题意,得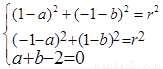 ﹍﹍﹍﹍﹍﹍﹍3分
﹍﹍﹍﹍﹍﹍﹍3分

又|AM|=|BM|=2,|PA|=|PB|, 所以S=2|PA|, ﹍﹍﹍﹍﹍﹍﹍8分
而|PA|=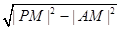 =
=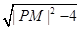 , 即S=2
, 即S=2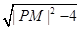 .
.
因此要求S的最小值,只需求|PM|的最小值即可,
即在直线3x+4y+8=0上找一点P,使得|PM|的值最小,﹍﹍﹍﹍﹍﹍﹍9分
所以|PM|min=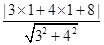 =3,
﹍﹍﹍﹍﹍﹍﹍10分
=3,
﹍﹍﹍﹍﹍﹍﹍10分
所以四边形PAMB面积的最小值为S=2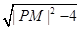 =2
=2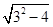 =2
=2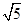 . ﹍﹍﹍12分
. ﹍﹍﹍12分
考点:圆的方程与直线与圆相切切线长问题
点评:待定系数法求圆的方程,求面积最小转化为利用图形求切线长最小

练习册系列答案
相关题目
 的方程为
的方程为 ,
,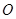 为坐标原点.
为坐标原点. 的圆
的圆 关于直线
关于直线 对称,并且满足
对称,并且满足 ,求
,求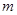 的值和直线
的值和直线 的方程;
的方程; 作直线与圆
作直线与圆 两点,求
两点,求 的最大面积以及此时直线
的最大面积以及此时直线 的斜率.
的斜率. 过点
过点 ,且与圆
,且与圆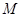 :
: 关于直线
关于直线 对称.
对称. 为圆
为圆 的最小值;
的最小值; 作两条相异直线分别与圆
作两条相异直线分别与圆 ,且直线
,且直线 和直线
和直线 的倾斜角互补,
的倾斜角互补, 为坐标原点,试判断直线
为坐标原点,试判断直线 和
和 是否平行?请说明理由.
是否平行?请说明理由.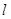 过点
过点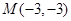 ,圆N:
,圆N: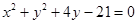 ,
,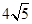 .
.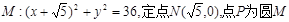 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足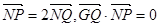 .
.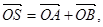 是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.