题目内容
设为a,b,c正数,记d为![]() ,
, ![]() ,
, ![]() 中的最小数.
中的最小数.
(1)求证:存在λ(0<λ<1=,使得d≤![]() ;......(*)
;......(*)
(2)求出使不等式(*)成立的最小正数λ并给予证明.
解析:(1)由d的定义知,d≤![]()
![]() ,d≤
,d≤![]()
![]() ,d≤
,d≤![]() .将这三个不等式相加,
.将这三个不等式相加,
得3d![]() ,即d≤
,即d≤![]() ,故可取λ=.
,故可取λ=.
(2)不妨设a≥b≥c.若b≤,则a≥2b-c>0,且d=![]() .因此5d-
.因此5d-![]() =
=
5![]() ≤5
≤5![]() -
-![]() =
=![]() ≤0,即λ≤.
≤0,即λ≤.
若b>,则a≤2b,且d=![]() .因此,
.因此,![]() =
=![]() =
=![]() =
=![]() ≤0,故此时也有λ≤.
≤0,故此时也有λ≤.
为了证明λ≥,我们取b=,则d=![]() ,此时有
,此时有![]() =
=![]() =
=![]() .由此可见,对于任意正数
.由此可见,对于任意正数

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 ,又
,又 最小值为
最小值为 ,则正数ω的值为
,则正数ω的值为



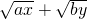 的最大值为
的最大值为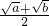

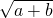
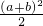
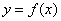 在
在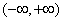 内有定义,对于给定的正数K,定义函数
内有定义,对于给定的正数K,定义函数 ,取函数
,取函数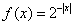 ,当K=
,当K= 时,函数
时,函数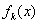 的单调递增区间为
的单调递增区间为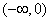 B
.
B
. C .
C . 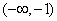 D.
D.