题目内容
按万有引力定律,两质点间的吸引力F=k| m1m2 | r2 |
分析:对力求定积分得到变力做的功;利用微积分基本定理求出定积分值即求出功.
解答:解:克服吸引力所作之功为
W=
k
dr(-km1m2
)
=km1m2(
-
)
故答案为:km1m2(
-
)
W=
| ∫ | b a |
| m1m2 |
| r2 |
| 1 |
| r |
| | | b a |
| 1 |
| a |
| 1 |
| b |
故答案为:km1m2(
| 1 |
| a |
| 1 |
| b |
点评:本题考查定积分在物理上的应用:对变力求定积分得到变力做的功、考查微积分基本定理.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 ,k为常数,m1,m2为两质点的质量,r为两点间距离,若两质点起始距离为a,质点m1沿直线移动至离m2的距离为b处(b>a),则克服吸引力所作之功为________.
,k为常数,m1,m2为两质点的质量,r为两点间距离,若两质点起始距离为a,质点m1沿直线移动至离m2的距离为b处(b>a),则克服吸引力所作之功为________.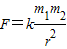 ,k为常数,m1,m2为两质点的质量,r为两点间距离,若两质点起始距离为a,质点m1沿直线移动至离m2的距离为b处(b>a),则克服吸引力所作之功为 .
,k为常数,m1,m2为两质点的质量,r为两点间距离,若两质点起始距离为a,质点m1沿直线移动至离m2的距离为b处(b>a),则克服吸引力所作之功为 .