题目内容
2012年7月2日,美国费米国家加速器实验室宣布,接近发现“上帝粒子”的存在,再次把人们的目光聚集在微观世界.按万有引力定律,两质点间的吸引力F=k
,k为常数,m1,m2分别为两质点的质量,r为两质点间的距离,若两质点起始距离为a,质点m1沿直线移动至离质点m2的距离为b处,则吸引力所做的功(b>a)为
| m1m2 |
| r2 |
km1m2(
-
)
| 1 |
| b |
| 1 |
| a |
km1m2(
-
)
.| 1 |
| b |
| 1 |
| a |
分析:设两质点间的距离为x,则引力F(x)=-
,吸引力所做的功即为F(x)在区间(a,b)上的定积分.
| km1m2 |
| x2 |
解答:解:设两质点间的距离为x,因为吸引力与质点移动方向相反,所以引力做负功,引力F(x)=-
,
所以吸引力所做的功为W=
F(x)dx=
dx=-km1m2(-
)
=-km1m2[-
-(-
)]=km1m2(
-
).
故答案为:km1m2(
-
).
| km1m2 |
| x2 |
所以吸引力所做的功为W=
| ∫ | b a |
| ∫ | b a |
| -km1m2 |
| x2 |
| 1 |
| x |
| | | b a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
故答案为:km1m2(
| 1 |
| b |
| 1 |
| a |
点评:本题考查了定积分在物理中的应用,本题要注意吸引力做的功为负功.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
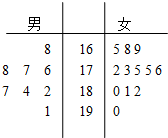 第30届奥运会将于2012年7月27日在伦敦举行,当地某学校招募了8名男志愿者和12名女志愿者.将这20名志愿者的身高如下茎叶图(单位:cm):
第30届奥运会将于2012年7月27日在伦敦举行,当地某学校招募了8名男志愿者和12名女志愿者.将这20名志愿者的身高如下茎叶图(单位:cm): 第30届夏季奥运会将于2012年7月27日在伦敦举行,当地某学校招募了8名男志愿者和12名女志愿者.将这20名志愿者的身高编成如茎叶图(单位:cm):若身高在180cm以上(包括l80cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.
第30届夏季奥运会将于2012年7月27日在伦敦举行,当地某学校招募了8名男志愿者和12名女志愿者.将这20名志愿者的身高编成如茎叶图(单位:cm):若身高在180cm以上(包括l80cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.