题目内容
若(| 3 | x |
| a |
| x |
分析:根据题意,首先得到(
+
)12的通项公式,先求得常数项的r的值,令其等于-220,解可得a的值.
| 3 | x |
| a |
| x |
解答:解:根据题意,(
+
)12的通项公式为Tr+1=Cnr(x
)n-r(
)br=ar•Cnr•x(4-
),
令4-
r=0?r=3
从而有arC123=-220;
解可得,a=-1;
故答案为:-1.
| 3 | x |
| a |
| x |
| 1 |
| 3 |
| a |
| x |
| 4r |
| 3 |
令4-
| 4 |
| 3 |
从而有arC123=-220;
解可得,a=-1;
故答案为:-1.
点评:本题考查二项式系数的性质,要求学生能写出该二项式的展开式,进而由根式与分数指数幂的互化、化简解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
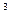 +3x
+3x +ax+b)e
+ax+b)e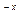 。
。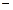 3 ,求f (x) 的单调区间;
3 ,求f (x) 的单调区间;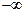 ,
,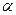 ),(2,
),(2,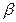 )上单调递增,在(
)上单调递增,在( )上单调递减,证明:
)上单调递减,证明: +3x
+3x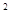 +ax+b)e
+ax+b)e 。
。 3 ,求f (x) 的单调区间;
3 ,求f (x) 的单调区间;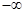 ,
, ),(2,
),(2, )上单调递增,在(
)上单调递增,在( )上单调递减,证明:
)上单调递减,证明: