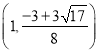题目内容
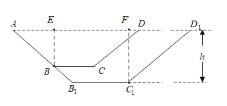
【题目】某农场灌溉水渠长为1000米,横截面是等腰梯形,如图,在等腰梯形![]() 中,
中,![]() ,
,![]() ,其中渠底
,其中渠底![]() 宽为1米,渠口
宽为1米,渠口![]() 宽为3米,渠深
宽为3米,渠深![]() 米.根据国家对农田建设补贴的政策,该农场计划在原水渠的基础上分别沿射线
米.根据国家对农田建设补贴的政策,该农场计划在原水渠的基础上分别沿射线![]() 方向加宽、
方向加宽、![]() 方向加深,若扩建后的水渠横截面
方向加深,若扩建后的水渠横截面![]() 仍是等腰梯形,且面积是原面积的2倍.设扩建后渠深为
仍是等腰梯形,且面积是原面积的2倍.设扩建后渠深为![]() 米,若挖掘费用为每立方米
米,若挖掘费用为每立方米![]() 万元,水渠的内壁(渠底和梯形两腰,
万元,水渠的内壁(渠底和梯形两腰,![]() 端也要重新铺设)铺设混凝土的费用为每平方米
端也要重新铺设)铺设混凝土的费用为每平方米![]() 万元.
万元.
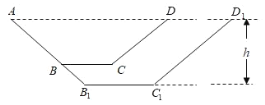
(1)用![]() 表示渠底
表示渠底![]() 的长度,并求出
的长度,并求出![]() 的取值范围;
的取值范围;
(2)问渠深![]() 为多少米时,建设费用最低?
为多少米时,建设费用最低?
【答案】(1)![]() ;
;![]() (2)当
(2)当![]() 米时,建设费用最低
米时,建设费用最低
【解析】
(1)作出梯形的高,根据相似三角形和等腰梯形的面积关系,即可求得![]() 的长度及
的长度及![]() 的取值范围;
的取值范围;
(2)得出建设费用关于![]() 的函数,利用导数求出函数的单调性,从而得出函数的极小值,即可得到答案.
的函数,利用导数求出函数的单调性,从而得出函数的极小值,即可得到答案.
(1)过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,
设扩建后渠底宽![]() 米,因为扩建后水渠仍为等腰梯形,渠深
米,因为扩建后水渠仍为等腰梯形,渠深![]() 米,
米,![]() ,所以
,所以![]() ,可得
,可得![]() ,
,![]() ,
,![]() 米,
米,
则![]() ,
,![]() ,
,
扩建后梯形![]() 的面积
的面积![]() .
.
又梯形![]() 的面积
的面积![]() ,因为
,因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
由 ,解得
,解得![]() ,
,
即![]() ,
,![]() ,
,
即渠底![]() 的长度为
的长度为![]() ,
, ![]() 的取值范围为
的取值范围为![]() .
.
(2)建设费用为![]()
![]()
![]()
![]() ,
, ,
,
设![]() ,
,
则![]()
![]() ,解得
,解得![]() .
.
|
| 1 |
|
| - | 0 | + |
|
|
|
所以当![]() 时,函数取得最小值,即建设费用最低.
时,函数取得最小值,即建设费用最低.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目