题目内容
【题目】已知函数![]() .
.
(1)若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,![]() 有两个不同的零点
有两个不同的零点![]() ,求证:
,求证:![]() .
.
【答案】(1)1;(2)证明见解析
【解析】
(1)求导得到![]() ,讨论
,讨论![]() 和
和![]() 两种情况,根据函数单调性得到
两种情况,根据函数单调性得到![]() ,解得答案.
,解得答案.
(2)要证明![]() ,只需要证明
,只需要证明![]() ,设
,设![]() ,求导得到单调性,得到
,求导得到单调性,得到![]() ,得到证明.
,得到证明.
(1)由已知得函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
且当![]() 时,
时,![]() ,不合题意;
,不合题意;
当![]() 时,由
时,由![]() 得
得![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,![]() 在
在![]() 处取到极小值,也是最小值
处取到极小值,也是最小值![]() ,由题意,
,由题意,![]() 恒成立,
恒成立,
令![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() ,即
,即![]() .
.
(2)![]() ,且
,且![]() 在
在![]() 处取到极小值1,
处取到极小值1,
又![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,故
,故![]() 且
且![]() ,
,
要证明:![]() ,只需证明
,只需证明![]() ,又
,又![]() ,
,
故只需证明:![]() ,即证:
,即证:![]() ,
,
即证:![]() ,即证:
,即证:![]() ,
,
设![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,由(1)知
,由(1)知![]() 恒成立,
恒成立,
所以![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() ,即命题成立.
,即命题成立.

【题目】某周末,郑州方特梦幻王国汇聚了八方来客.面对该园区内相邻的两个主题公园“千古蝶恋”和“西游传说”,成年人和未成年人选择游玩的意向会有所不同.某统计机构对园区内的100位游客(这些游客只在两个主题公园中二选一)进行了问卷调查.调查结果显示,在被调查的50位成年人中,只有10人选择“西游传说”,而选择“西游传说”的未成年人有20人.
(1)根据题意,请将下面的![]() 列联表填写完整;
列联表填写完整;
选择“西游传说” | 选择“千古蝶恋” | 总计 | |
成年人 | |||
未成年人 | |||
总计 |
(2)根据列联表的数据,判断是否有![]() 的把握认为选择哪个主题公园与年龄有关.
的把握认为选择哪个主题公园与年龄有关.
附参考公式与表: (
(![]() ).
).
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)司机师傅小李准备在一辆开了![]() 年的
年的![]() 型车和一辆开了
型车和一辆开了![]() 年的
年的![]() 型车中选择,为了尽最大可能实现
型车中选择,为了尽最大可能实现![]() 年内(含
年内(含![]() 年)不换车,试通过计算说明,他应如何选择.
年)不换车,试通过计算说明,他应如何选择.
附: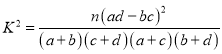 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |