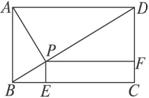
题目内容
在矩形ABCD中,AB=4,AD=6,在该矩形内任取一点P,则使∠APB≥
的概率为( )
| π |
| 2 |
A、
| ||
B、1-
| ||
C、1-
| ||
D、
|
分析:先明确是一个几何概型中的面积类型,然后分别求得阴影部分的面积和矩形的面积,再用概率公式求两者的比值即为所求的概率.
解答: 解:如图:以AB为直径作半圆,则当点P落在半圆的内部(包括边界)时∠APB≥
解:如图:以AB为直径作半圆,则当点P落在半圆的内部(包括边界)时∠APB≥
,
故所求的概率P(A)=
=
.
故选D.
 解:如图:以AB为直径作半圆,则当点P落在半圆的内部(包括边界)时∠APB≥
解:如图:以AB为直径作半圆,则当点P落在半圆的内部(包括边界)时∠APB≥| π |
| 2 |
故所求的概率P(A)=
| ||
| 6×4 |
| π |
| 12 |
故选D.
点评:本题主要考查几何概型中的面积类型,基本方法是:分别求得构成事件A的区域面积和试验的全部结果所构成的区域面积,两者求比值,即为概率,还考查了定积分的应用在几何上的应用(求封闭图形的面积).

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在矩形ABCD中,已知AD=2,AB=a(a>2),E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积.
如图,在矩形ABCD中,已知AD=2,AB=a(a>2),E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积.