题目内容
【题目】设点![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,
,![]() 与
与![]() 交于另一点为
交于另一点为![]() .若以点
.若以点![]() 为圆心,以线段
为圆心,以线段![]() 长为半径的圆与
长为半径的圆与![]() 有4个公共点,求
有4个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用相关点法求出![]() 的方程;(2)由
的方程;(2)由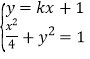 得
得![]() ,设
,设![]() ,
,![]() ,
,![]() ,则点
,则点![]() 的轨迹方程为
的轨迹方程为![]() ,
,
由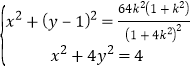 ,得
,得![]() ,(
,(![]() )(*)依题意得,(*)式关于
)(*)依题意得,(*)式关于![]() 的方程在
的方程在![]() 有两个不同的实数解,利用二次函数有关知识即可求出
有两个不同的实数解,利用二次函数有关知识即可求出![]() 的取值范围.
的取值范围.
试题解析:
(1)设点![]() ,
,![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以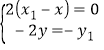 ,解得
,解得![]() ,
,
由于点![]() 在圆
在圆![]() 上,所以
上,所以![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)由(1)知,![]() 的方程为
的方程为![]() ,因为直线
,因为直线![]() .
.
由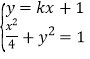 得
得![]() ,
,
设![]() ,
,![]() ,因此
,因此![]() ,
,![]() ,
,
![]() ,
,
则点![]() 的轨迹方程为
的轨迹方程为![]() ,
,
由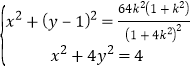 ,得
,得![]() ,(
,(![]() )(*)
)(*)
依题意得,(*)式关于![]() 的方程在
的方程在![]() 有两个不同的实数解,
有两个不同的实数解,
设![]() ,
,
因为函数![]() 的对称轴为
的对称轴为![]() ,
,
要使函数![]() 的图象在
的图象在![]() 与
与![]() 轴有两个不同的交点,
轴有两个不同的交点,
则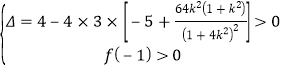 ,
,
整理得: ,即
,即![]() ,
,
所以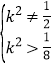 .
.
解得![]() ,
,
所以![]() 的取值范围为
的取值范围为![]()

练习册系列答案
相关题目