题目内容
已知圆的极坐标方程为
．
（1）将圆的极坐标方程化为普通方程，并选择恰当的参数写出它的参数方程；
（2）若点P（x，y）在该圆上，求
的最大值和最小值．
解：（1）由，得
利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2代换，
x2+y2+2x-2
y-5=0，整理（x+1）2+（y-）2=9
它的参数方程
（α为参数）．
（2）若点P（x，y）在该圆上，利用圆的参数方程可得
=3sinα+3cosα+2=6sin（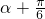
）+2，
当sin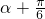（）=1时，取得最大值8，当sin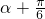（）=-1时，取得最小值-4
分析：（1）利用直角坐标与极坐标间的关系：ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得．
（2）由（1）参数方程（α为参数），得出=3sinα+3cosα+2=6sin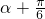（）+2，利用三角函数的性质求解．
点评：本题考查极坐标方程，参数方程和直角坐标方程的互化，圆的参数方程的应用，三角函数的性质．属于中档题．
，得利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2代换，
x2+y2+2x-2
y-5=0，整理（x+1）2+（y-）2=9它的参数方程
（α为参数）．（2）若点P（x，y）在该圆上，利用圆的参数方程可得
=3sinα+3cosα+2=6sin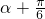（）+2，当sin（
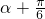）=1时，取得最大值8，当sin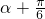（）=-1时，取得最小值-4分析：（1）利用直角坐标与极坐标间的关系：ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得．
（2）由（1）参数方程
（α为参数），得出=3sinα+3cosα+2=6sin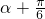（）+2，利用三角函数的性质求解．点评：本题考查极坐标方程，参数方程和直角坐标方程的互化，圆的参数方程的应用，三角函数的性质．属于中档题．
练习册系列答案
相关题目
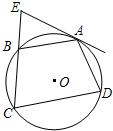A．如图，四边形ABCD内接于⊙O，弧AB=弧AD，过A点的切线交CB的延长线于E点．