题目内容
已知圆的极坐标方程为ρ=5| 3 |
分析:把圆的极坐标方程化为直角坐标方程,求出圆心坐标,与半径,依据直角坐标与极坐标的互化公式,把圆心的直角坐标化为极坐标.
解答:解:由题意ρ=5
cosθ-5sinθ可表示为ρ2=5
ρcosθ-5ρsinθ,
化为直角坐标方程为x2+y2-5
x+5y=0,即(x-
)2+(y+
)2=25,
因此该圆的半径为5,圆心的直角坐标为(
,-
);
所以圆的半径为5,圆心的极坐标为(5,-
).
| 3 |
| 3 |
化为直角坐标方程为x2+y2-5
| 3 |
5
| ||
| 2 |
| 5 |
| 2 |
因此该圆的半径为5,圆心的直角坐标为(
5
| ||
| 2 |
| 5 |
| 2 |
所以圆的半径为5,圆心的极坐标为(5,-
| π |
| 6 |
点评:本题考查把极坐标方程化为直角坐标方程的方法,以及求点的极坐标的方法,关键是利用公式x=ρcosθ,y=ρsinθ,ρ=
,tanθ=
.
| x2+ y2 |
| y |
| x |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
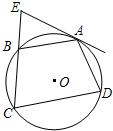 A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.
A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.