题目内容
设函数 (
( ).
).
(1)若 为偶函数,求实数
为偶函数,求实数 的值;
的值;
(2)已知 ,若对任意
,若对任意 都有
都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)0;(2)
解析试题分析:(1)根据偶函数定义 ,得到
,得到 ,平方后可根据对应系数相等得到a的值,也可将上式两边平方得
,平方后可根据对应系数相等得到a的值,也可将上式两边平方得 恒成立,得a的值。(2)应先去掉绝对值将其改写为分段函数,在每段上求函数
恒成立,得a的值。(2)应先去掉绝对值将其改写为分段函数,在每段上求函数 在
在 时的最小值,在每段求最值时都属于定轴动区间问题,需讨论。最后比较这两个最小值的大小取最小的那个,即为原函数的最小值。要使
时的最小值,在每段求最值时都属于定轴动区间问题,需讨论。最后比较这两个最小值的大小取最小的那个,即为原函数的最小值。要使 恒成立,只需
恒成立,只需 的最小值大于等于1即可,从而求得a的范围
的最小值大于等于1即可,从而求得a的范围
试题解析:(1)若 的为偶函数,则
的为偶函数,则
 ,
, ,
,
故 ,
,
两边平方得 ,展开
,展开 时,
时, 为偶函数。
为偶函数。
(2)
设 ,
,
①求 ,即
,即 的最小值:
的最小值:
若 ,
, ;
;
若 ,
,
②求 ,即
,即 的最小值
的最小值 ,
,
比较 与
与 ,
, 的大小:
的大小:
 ,故
,故
“ 对
对 恒成立”即为“
恒成立”即为“ (
( )”
)”
令 ,解得
,解得 。
。
考点:奇偶性,恒成立问题

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 的定义域为
的定义域为 .设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
.设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N. 是定值;
是定值; 有最大值还是最小值,并求出此最大值或最小值.
有最大值还是最小值,并求出此最大值或最小值. ,
, ,求方程
,求方程 的根;
的根; 满足
满足 ,求函数在
,求函数在 的值域.
的值域. (
( 为实常数).
为实常数). 图像上动点
图像上动点 到定点
到定点 的距离的最小值为
的距离的最小值为 ,求实数
,求实数 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数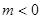 ,若不等式
,若不等式 在
在 有解,求
有解,求 的取值范围.
的取值范围. (
( )
) 是定义在R上的偶函数,求a的值;
是定义在R上的偶函数,求a的值; 对任意
对任意 ,
, 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是 元.
元. 是定义在(-1,1)上的奇函数,其中
是定义在(-1,1)上的奇函数,其中 ,a为正整数,且满足
,a为正整数,且满足 .
. 的解析式;
的解析式; 的
的 的范围;
的范围; 同时满足以下三个条件时称
同时满足以下三个条件时称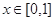 ,总有
,总有 ;
; 成立,则下列判断正确的有 .
成立,则下列判断正确的有 . ;
; 在区间[0,1]上是“友谊函数”;
在区间[0,1]上是“友谊函数”; <
< ≤1,则
≤1,则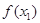 ≤
≤ .
.  为定义域
为定义域 上的单调函数,且存在区间
上的单调函数,且存在区间 (其中
(其中 ,使得当
,使得当 时,
时,  ,则称函数
,则称函数 是
是 上的正函数,求
上的正函数,求 ,使得函数
,使得函数 是
是 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数