题目内容
已知数列 的首项
的首项 ,前
,前 项和
项和 .(Ⅰ)求数列
.(Ⅰ)求数列 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设 ,
, ,
, 为数列
为数列 的前
的前 项和,求证:
项和,求证: .
.
 的首项
的首项 ,前
,前 项和
项和 .(Ⅰ)求数列
.(Ⅰ)求数列 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设 ,
, ,
, 为数列
为数列 的前
的前 项和,求证:
项和,求证: .
.解 (Ⅰ)由题设得
 ,即
,即 .
.(Ⅱ)当
 时,
时, ;
;当
 时,
时, =
= =
= ;
;由于此时-2×1+13=11=
 ,从而数列
,从而数列 的通项公式是
的通项公式是 .
.(Ⅲ)由(Ⅱ)知,
 ,数列
,数列 从第7项起均为负数.设数列
从第7项起均为负数.设数列 的前n项的和为
的前n项的和为 .
.当
 时,
时, =
= =
= ;
;当
 时,
时,

=

=

=
 =
= .
.所以数列
 的前n项的和为
的前n项的和为
本试题主要是考查了数列的前n项和与通项公式之间关系的运用。以及数列的前n项和的运用。

练习册系列答案
相关题目
 的前
的前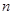 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
. (
( N*).
N*). ;
; .
. 中,
中, ,则
,则 ( )
( )



 ,
,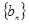 满足:
满足: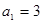 ,当
,当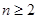 时,
时,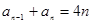 ;对于任意的正整数
;对于任意的正整数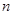 ,
,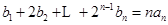 .设
.设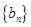 的前
的前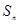 .
.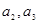 ,并求数列
,并求数列
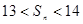 的
的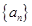 是以2为首项,1为公差的等差数列,数列
是以2为首项,1为公差的等差数列,数列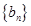 是以1为首项,2为公比的等比数列, 则
是以1为首项,2为公比的等比数列, 则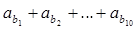 = .
= .  的前
的前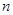 项和是
项和是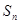 ,满足
,满足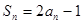 .
.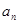 及前
及前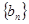 满足
满足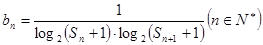 ,求数列
,求数列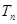 ;
;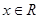 ,恒有
,恒有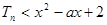 成立,求实数
成立,求实数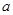 的取值范围
的取值范围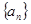 (
(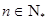 )中,已知
)中,已知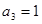 ,
,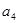 是
是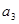 和
和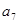 的等比中项.
的等比中项.
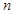 项和为
项和为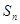 ,求使
,求使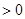 时
时 }的前n项和
}的前n项和 满足:
满足: ,且
,且 =1.那么
=1.那么 =
=