题目内容
实数一元二次方程x2+ax+2b=0有两个根,一个根在区间(0,1)内,另一个根在区间(1,2)内,
(1)求点(a,b)对应的区域的面积;
(2 )求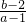 的取值范围.
的取值范围.
解:(1)构造函数f(x)=x2+ax+2b
∵一元二次方程x2+ax+2b=0有两个根,一个根在区间(0,1)内,另一个根在区间(1,2)内
∴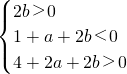
对应的区域如图所示

由 ,可得a=-3,b=1,
,可得a=-3,b=1,
∴点(a,b)对应的区域的面积为 =1;
=1;
(2 )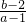 表示(a,b)与点(1,2)连线的斜率
表示(a,b)与点(1,2)连线的斜率
由(-3,1),(1,2)可得斜率为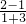 =
= ;由(-1,0),(1,2)可得斜率为
;由(-1,0),(1,2)可得斜率为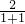 =1
=1
∴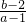 的取值范围为(
的取值范围为( ,1).
,1).
分析:(1)构造函数f(x)=x2+ax+2b,利用零点存在定理,建立不等式组,确定平面区域,即可求得点(a,b)对应的区域的面积;
(2)明确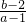 的几何意义,求出斜率,即可求
的几何意义,求出斜率,即可求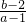 的取值范围.
的取值范围.
点评:本题主要考查了一元二次方程根的分布,以及线性规划的基本知识,考查数形结合的数学思想,属于中档题.
∵一元二次方程x2+ax+2b=0有两个根,一个根在区间(0,1)内,另一个根在区间(1,2)内
∴
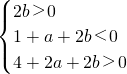
对应的区域如图所示

由
 ,可得a=-3,b=1,
,可得a=-3,b=1,∴点(a,b)对应的区域的面积为
 =1;
=1;(2 )
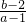 表示(a,b)与点(1,2)连线的斜率
表示(a,b)与点(1,2)连线的斜率由(-3,1),(1,2)可得斜率为
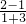 =
= ;由(-1,0),(1,2)可得斜率为
;由(-1,0),(1,2)可得斜率为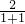 =1
=1∴
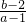 的取值范围为(
的取值范围为( ,1).
,1).分析:(1)构造函数f(x)=x2+ax+2b,利用零点存在定理,建立不等式组,确定平面区域,即可求得点(a,b)对应的区域的面积;
(2)明确
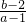 的几何意义,求出斜率,即可求
的几何意义,求出斜率,即可求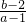 的取值范围.
的取值范围.点评:本题主要考查了一元二次方程根的分布,以及线性规划的基本知识,考查数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
 的取值范围.
的取值范围.