题目内容
如图,是半径为2的一个半圆,O为圆心,A、B是直径的两个端点,M、N为半圆弧上的两个动点(点M不与A重合),点P在半径OA上,OP=a(a为定值),其中0<a<2,∠AOM=2∠BPN,直线PN与OM相交于点Q.能否找到两条相交直线,使动点Q到这两条直线的距离之积为定值?若能,请求出这个定值;若不能,请说明理由.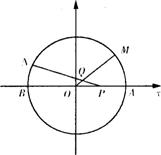
答案:解:以O为坐标原点,AB所在的直线为x轴建立直角坐标系,
则半圆O的方程为x2+y2=4(y≥0),
设∠AOM=2α(0<2α≤π),则∠BPN=α,
∠APN=π-α,点M坐标为(2cos2α,2sin2α),
直线OM的方程为y=xtan2α,
直线PN的方程为y=-(x-a)tanα,
由以上两方程消去α,
可得y[1-![]() ]=
]=![]() ,
,
即1-![]() =
=![]() ,
,
也即(x-a)2-y2=-2x(x-a),
即3(x-![]() a)2-y2=
a)2-y2=![]() ,
,
由此可知点Q在双曲线3(x-![]() a)2-y2=
a)2-y2=![]() 上运动.
上运动.
而该双曲线的渐近线方程为3(x-![]() )2-y2=0,
)2-y2=0,
即y=![]() (x-
(x-![]() a).
a).
设Q(x,y)到两渐近线的距离分别为d1、d2,则3(x-![]() )2-y2=
)2-y2=![]() 总成立.
总成立.
且d1·d2=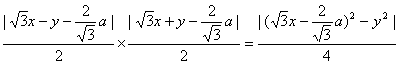
=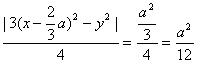 .
.

练习册系列答案
相关题目

 (2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED与弧EC交于点G,且EG=
(2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED与弧EC交于点G,且EG=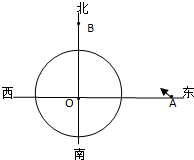 如图,一艘轮船在A处正沿直线返回港口B,接到气象台的台风预报,台风中心O位于轮船正西40km处,受影响的范围是半径为20km的圆形区域.已知港口B位于台风中心正北30km处.
如图,一艘轮船在A处正沿直线返回港口B,接到气象台的台风预报,台风中心O位于轮船正西40km处,受影响的范围是半径为20km的圆形区域.已知港口B位于台风中心正北30km处. (2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED 与弧EC交于点G,且cos∠CBG=
(2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED 与弧EC交于点G,且cos∠CBG=