题目内容
证明数列{an}为等差数列的充要条件是{an}的前n项和Sn=An2+Bn.
证明:充分性:由{an}的前n项Sn=An2+Bn,?
∴n≥2时,an=Sn-Sn-1=An2+Bn-[A(n-1)2+B(n-1)]
=2A·n+B-A?
∵a1=S1=A+B满足上式,?
∴an=2An+B-A,n∈N*,?
∴an+1-an=[2A(n+1)+B-A]-[2An+B-A]=?2A,
∴{an}为等差数列.?
必要性:∵{an}是等差数列,?
∴Sn=na1+![]() n(n-1)d
n(n-1)d
=![]() n2+(a1-
n2+(a1-![]() )n?
)n?
令![]() =A,a1-
=A,a1-![]() =B,
=B,
∴Sn=An2+Bn.?
综上,数列{an}为等差数列的充要条件是Sn=An2+Bn.

练习册系列答案
相关题目
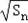 是an+2 和an的等比中项.
是an+2 和an的等比中项.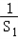 +
+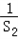 +…+
+…+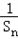 <1;
<1;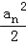 恒成立,求这样的正整数m共有多少个?
恒成立,求这样的正整数m共有多少个? 是an+2 和an的等比中项.
是an+2 和an的等比中项. +
+ +…+
+…+ <1;
<1; 恒成立,求这样的正整数m共有多少个?
恒成立,求这样的正整数m共有多少个? 是an+2 和an的等比中项.
是an+2 和an的等比中项. +
+ +…+
+…+ <1;
<1; 恒成立,求这样的正整数m共有多少个?
恒成立,求这样的正整数m共有多少个?