题目内容
(理)椭圆 上的点到直线
上的点到直线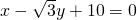 的最近距离d=
的最近距离d=
- A.4
- B.

- C.
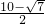
- D.
C
分析:设椭圆 上的点P(2cosθ,sinθ),利用点到直线间的距离公式
上的点P(2cosθ,sinθ),利用点到直线间的距离公式 =
= 即可得到所求答案.
即可得到所求答案.
解答:∵椭圆 的参数方程为:
的参数方程为: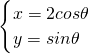 ,
,
∴设椭圆 上的点P(2cosθ,sinθ),
上的点P(2cosθ,sinθ),
则点P到直线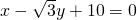 的距离
的距离 =
= (tanφ=-
(tanφ=- ),
),
∴dmin=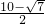 .
.
故选C.
点评:本题考查直线与圆锥曲线的关系,解决的关键在于根据椭圆的参数方程设出椭圆 上的点P(2cosθ,sinθ),着重考查点到直线的距离公式,属于中档题.
上的点P(2cosθ,sinθ),着重考查点到直线的距离公式,属于中档题.
分析:设椭圆
 上的点P(2cosθ,sinθ),利用点到直线间的距离公式
上的点P(2cosθ,sinθ),利用点到直线间的距离公式 =
= 即可得到所求答案.
即可得到所求答案.解答:∵椭圆
 的参数方程为:
的参数方程为: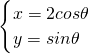 ,
,∴设椭圆
 上的点P(2cosθ,sinθ),
上的点P(2cosθ,sinθ),则点P到直线
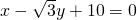 的距离
的距离 =
= (tanφ=-
(tanφ=- ),
),∴dmin=
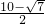 .
.故选C.
点评:本题考查直线与圆锥曲线的关系,解决的关键在于根据椭圆的参数方程设出椭圆
 上的点P(2cosθ,sinθ),着重考查点到直线的距离公式,属于中档题.
上的点P(2cosθ,sinθ),着重考查点到直线的距离公式,属于中档题. 
练习册系列答案
相关题目
