题目内容
椭圆G:(1)求离心率e的取值范围.
(2)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为![]() .
.
①求此时椭圆G的方程;
②(理)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点P(0,![]() )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
)、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
(文)设斜率为1的直线与椭圆G相交于不同的两点A、B,Q为AB的中点,点P的坐标为(0![]() ),若直线PQ垂直平分弦AB,求AB所在的直线方程.
),若直线PQ垂直平分弦AB,求AB所在的直线方程.
答案:解:(1)设M(x0,y0),∵M∈G,∴![]() =1.①
=1.①
又![]() =0,∴(x0+c,y0)·(x0-c,y0)=0.②
=0,∴(x0+c,y0)·(x0-c,y0)=0.②
由②得y02=c2-x02代入①式整理,得x02=a2(2![]() ).又0≤x02≤a2,∴0≤a2(2
).又0≤x02≤a2,∴0≤a2(2![]() )≤a2.解得(
)≤a2.解得(![]() )2≥
)2≥![]() ,即e2≥
,即e2≥![]() .又0<e<1,∴e∈[
.又0<e<1,∴e∈[![]() ,1).
,1).
(2)①当e=![]() 时,设椭圆G方程为
时,设椭圆G方程为![]() ,
,
设H(x,y)为椭圆上一点,则|HN|2=x2+(y-3)2=-(y+3)2+2b2+18,其中-b≤y≤b.若0<b<3,则当y=-b时,|HN|2有最大值b2+6b+9.由b2+6b+9=50,得b=-3±![]() (舍去);
(舍去);
若b≥3,当y=-3时,|HN|2有最大值2b2+18.由2b2+18=50,得b2=16.∴所求椭圆方程为![]() .
.
②(理)设A(x1,y1)、B(x2,y2)、Q(x0,y0),则由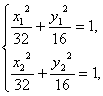 两式相减,得x0+2ky0=0,③
两式相减,得x0+2ky0=0,③
又直线PQ⊥直线l,∴直线PQ方程为y=![]() ,将点Q(x0,y0)代入上式,得y0=
,将点Q(x0,y0)代入上式,得y0=![]() .④
.④
由③④,得Q(![]() ).
).
方法一:而Q点必在椭圆内部,∴![]() <1.由此得k2<
<1.由此得k2<![]() .又k≠0,∴
.又k≠0,∴![]() <k<0或0<k<
<k<0或0<k<![]() .故当k∈(
.故当k∈(![]() ,0)∪(0,
,0)∪(0,![]() )时,A、B两点关于过点P、Q的直线对称.
)时,A、B两点关于过点P、Q的直线对称.
方法二:∴AB所在直线方程为y+![]() =k(x
=k(x![]() k).
k).
由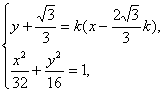 得(1+2k2)x2
得(1+2k2)x2![]() k(1+2k2)x+
k(1+2k2)x+![]() (1+2k2)2-32=0.
(1+2k2)2-32=0.
显然1+2k2≠0,而Δ=[![]() k(1+2k2)]2-4(1+2k2)[
k(1+2k2)]2-4(1+2k2)[![]() (1+2k2)2-32]=-4(1+2k2)[
(1+2k2)2-32]=-4(1+2k2)[![]() (1+2k2)-32].
(1+2k2)-32].
∵直线l与椭圆有两个不同的交点A、B,∴Δ>0.解得k2<![]() .又k≠0,∴
.又k≠0,∴![]() <k<0或0<k<
<k<0或0<k<![]() .故当k∈(
.故当k∈(![]() ,0)∪(0,
,0)∪(0,![]() )时,A、B两点关于过点P、Q的直线对称.
)时,A、B两点关于过点P、Q的直线对称.
另解:设直线l的方程为y=kx+b,由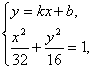 得(1+2k2)x2+4kbx+2b2-32=0.(*)
得(1+2k2)x2+4kbx+2b2-32=0.(*)
设A(x1,y1)、B(x2,y2)、Q(x0,y0),则x0=![]() ,y0=kx0+b=
,y0=kx0+b=![]() .③
.③
又直线PQ⊥直线l,∴直线PQ的方程为y=![]() .将Q(x0,y0)代入上式,得y0=
.将Q(x0,y0)代入上式,得y0=![]() x0+
x0+![]() .④
.④
将③代入④,得b=-![]() (1+2k2).⑤
(1+2k2).⑤
∵x1、x2是(*)的两根,∴Δ=(4kb)2-4(1+2k2)(2b2-32)=8×16(1+2k2)-8b2≥0.⑥
⑤代入⑥,得k2<![]() .
.
又k≠0,∴当k∈(![]() ,0)∪(0,
,0)∪(0,![]() )时,A、B两点关于过点P、Q的直线对称.
)时,A、B两点关于过点P、Q的直线对称.
(文)设A(x1,y1)、B(x2,y2)、Q(x0,y0),则由 ,两式相减,得x0+2y0=0.③
,两式相减,得x0+2y0=0.③
又直线PQ⊥直线l,∴直线PQ的方程为y=-x+![]() .将点Q(x0,y0)代入上式,得y0=-x0+
.将点Q(x0,y0)代入上式,得y0=-x0+![]() .④
.④
由③④,得Q(![]() ,-
,-![]() ),
),
∴直线AB的方程为y+![]() =1×(x
=1×(x![]() ),即x-y-
),即x-y-![]() =0.
=0.
另解:设直线l的方程为y=x+b,由 ,得3x2+4bx+2b2-32=0.(*)
,得3x2+4bx+2b2-32=0.(*)
设A(x1,y1)、B(x2,y2)、Q(x0,y0),则x0=![]() ,y0=x0+b=
,y0=x0+b=![]() .③
.③
又直线PQ⊥直线l,∴直线PQ的方程为y=-x+![]() .将Q(x0,y0)代入上式,得y0=-x0+
.将Q(x0,y0)代入上式,得y0=-x0+![]() .④
.④
将③代入④,得b![]() .
.
此时,Δ=(4b)2-4×3(2b2-32)=-8b2+12×32=300>0.
∴b=![]() 符合要求.
符合要求.
∴直线AB的方程为y=x![]() ,即x-y
,即x-y![]() =0.
=0.

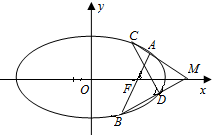 已知椭圆G:
已知椭圆G: