题目内容
已知向量 ,函数f(x)=
,函数f(x)= •
• .
.
(1)若 ,求函数f(x)的值;
,求函数f(x)的值;
(2)将函数f(x)的图象按向量 =(m,n)(0<m<π)平移,使得平移后的图象关于原点对称,求向量
=(m,n)(0<m<π)平移,使得平移后的图象关于原点对称,求向量 .
.
解:由题意,得 =
=
=
= (5分)
(5分)
(1)∵x∈[ ,π],cosx=-
,π],cosx=- ,∴sinx=
,∴sinx= ,
,
∴ (7分)
(7分)
(2)由图象变换得,平移后的函数为 ,
,
而平移后的图象关于原点对称,
∴ ,(9分)
,(9分)
即 ,
,
即 .
.
分析:求出函数f(x)= •
• .的最简形式:
.的最简形式:
(1)根据x的范围,利用 ,求出sinx=
,求出sinx= ,得到函数f(x)的值.
,得到函数f(x)的值.
(2)由图象变换得,平移后的函数为 ,而平移后的图象关于原点对称,g(0)=0求出n,
,而平移后的图象关于原点对称,g(0)=0求出n,
推出m,求向量 .
.
点评:本题考查平面向量数量积的运算,函数y=Asin(ωx+φ)的图象变换,向量间的变换,考查计算能力.
 =
=
=

=
 (5分)
(5分)(1)∵x∈[
 ,π],cosx=-
,π],cosx=- ,∴sinx=
,∴sinx= ,
,∴
 (7分)
(7分)(2)由图象变换得,平移后的函数为
 ,
,而平移后的图象关于原点对称,
∴
 ,(9分)
,(9分)即
 ,
,即
 .
.分析:求出函数f(x)=
 •
• .的最简形式:
.的最简形式:(1)根据x的范围,利用
 ,求出sinx=
,求出sinx= ,得到函数f(x)的值.
,得到函数f(x)的值.(2)由图象变换得,平移后的函数为
 ,而平移后的图象关于原点对称,g(0)=0求出n,
,而平移后的图象关于原点对称,g(0)=0求出n,推出m,求向量
 .
.点评:本题考查平面向量数量积的运算,函数y=Asin(ωx+φ)的图象变换,向量间的变换,考查计算能力.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
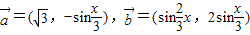 ,函数f(x)=
,函数f(x)=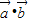 .
.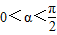 且
且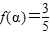 ,求
,求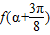 的值.
的值.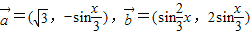 ,函数f(x)=
,函数f(x)=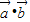 .
.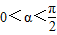 且
且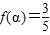 ,求
,求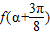 的值.
的值.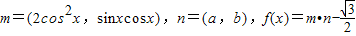 ,函数f(x)的图象关于直线
,函数f(x)的图象关于直线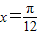 对称,且
对称,且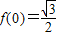
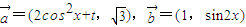 ,函数f(x)=
,函数f(x)=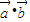 .
.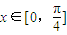 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.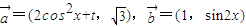 ,函数f(x)=
,函数f(x)=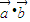 .
.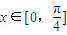 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.