题目内容
已知实数a,b满足-1≤a≤1,0≤b≤1,则函数f(x)=x3-ax2+bx无极值的概率是 .
考点:几何概型,函数在某点取得极值的条件
专题:导数的综合应用,概率与统计
分析:求出函数无极值的等价条件,利用积分求出阴影部分的面积,结合几何槪型的概率公式即可得到结论.
解答:
解:函数f(x)=x3-ax2+bx的导数f′(x)=3x2-2ax+b,
若函数f(x)=x3-ax2+bx无极值,
则f′(x)=3x2-2ax+b≥0恒成立,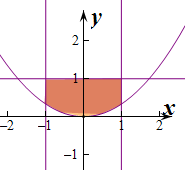
即△=4a2-12b≤0,即a2≤3b,
作出不等式对应的平面区域如图;
则阴影部分的面积S=
(1-
)dx=(x-
x3)|
=2-
=
,
则由几何槪型的概率公式可得函数f(x)=x3-ax2+bx无极值的概率P=
=
=
=
,
故答案为:
若函数f(x)=x3-ax2+bx无极值,
则f′(x)=3x2-2ax+b≥0恒成立,
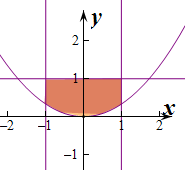
即△=4a2-12b≤0,即a2≤3b,
作出不等式对应的平面区域如图;
则阴影部分的面积S=
| ∫ | 1 -1 |
| x2 |
| 3 |
| 1 |
| 9 |
1 -1 |
| 2 |
| 9 |
| 16 |
| 9 |
则由几何槪型的概率公式可得函数f(x)=x3-ax2+bx无极值的概率P=
| S阴影部分 |
| S矩形 |
| ||
| 2×1 |
| 16 |
| 18 |
| 8 |
| 9 |
故答案为:
| 8 |
| 9 |
点评:本题主要考查几何槪型的概率计算,利用函数无价值以及利用积分求出对应区域的面积是解决本题的关键,涉及的知识点较多,综合性较强.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图所示,在三棱柱ABC-A1B1C1中,M、N分别是BC和A1B1的中点.
如图所示,在三棱柱ABC-A1B1C1中,M、N分别是BC和A1B1的中点. 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.则样本的平均值是
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.则样本的平均值是