题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
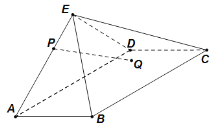
(Ⅱ)已知椭圆的左焦点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() (
(![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.
(ⅰ)若![]() ,求
,求![]() 的面积;
的面积;
(ⅱ)直线![]() 是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
【答案】见解析
【解析】(Ⅰ)由椭圆的离心率![]() ,可得
,可得![]() .
.
所以![]() ,所以
,所以![]() .
.
又因为点![]() 在椭圆上,
在椭圆上,
所以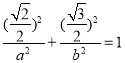 ,即
,即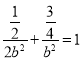 ,解得
,解得![]() ,故
,故![]() .
.
∴椭圆![]() 的方程为
的方程为![]() . -----------------4分
. -----------------4分
(Ⅱ)椭圆的左焦点为![]() .
.
(ⅰ)当![]() 时,
时,![]() .
.
故直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
由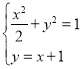 ,消元得
,消元得![]() ,解得
,解得![]() 或
或![]() .
.
由题意可得![]() ,故点
,故点![]() 的坐标为
的坐标为![]() .
.
由/span>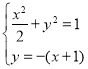 ,消元得
,消元得![]() ,解得
,解得![]() 或
或![]() .
.
由题意可得![]() ,故点
,故点![]() 的坐标为
的坐标为![]() .
.
所以点![]() 到直线
到直线![]() 的距离
的距离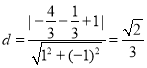 .
.
而![]() ,所以
,所以![]() 的面积
的面积![]() .--------------- 8分
.--------------- 8分
(ⅱ)设直线![]() 方程为
方程为![]() ,
,![]() ,
,![]() .
.
联立方程组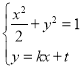 ,消去
,消去![]() ,得
,得![]() ,-------------10分
,-------------10分
由根与系数的关系可得![]() ,
,![]() .
.
所以![]()
![]()
![]() ,
,
所以![]() ,即
,即![]() ,
,
代入整理,![]() ,即
,即![]() . -----------------13分
. -----------------13分
所以直线![]() 的方程为
的方程为![]() ,所以直线
,所以直线![]() 总过定点
总过定点![]() . -----------------14分
. -----------------14分
【命题意图】本题考查椭圆的方程与性质、直线和椭圆的位置关系、三角形面积的求解以及定点的探究性问题,意在考查基本的逻辑推理能力、运算能力和数学应用意识等.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目